如图所示,已知空间四边形 的每条边和对角线长都等于1,点
的每条边和对角线长都等于1,点 ,
, ,
, 分别是
分别是 、
、 、
、 的中点,计算:
的中点,计算:
(1) ;
;
(2) 的长;
的长;
(3)异面直线 与
与 所成角的余弦值.
所成角的余弦值.
如图所示, 为正方体,给出以下五个结论:
为正方体,给出以下五个结论:
① 平面
平面 ;
;
② 平面
平面 ;
;
③ 与底面
与底面 所成角的正切值是
所成角的正切值是 ;
;
④二面角 的正切值是
的正切值是 ;
;
⑤过点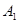 且与异面直线
且与异面直线 和
和 均成
均成 角的直线有2条.
角的直线有2条.
其中,所有正确结论的序号为_______.
如图所示,M、N、P分别是正方体ABCD-A1B1C1D1的棱AB、BC、DD1上的点.
(Ⅰ)若 ,求证:无论点P在DD1上如何移动,总有BP⊥MN;
,求证:无论点P在DD1上如何移动,总有BP⊥MN;
(Ⅱ)棱DD1上是否存在这样的点P,使得平面APC1⊥平面A1ACC1?证明你的结论.
如图(1)示,在梯形 中,
中, ,
, ,且
,且 ,如图(2)沿
,如图(2)沿 将四边形
将四边形 折起,使得平面
折起,使得平面 与平面
与平面 垂直,
垂直, 为
为 的中点.
的中点.
(Ⅰ)求证:
(Ⅱ)求证: ;
;
(Ⅲ)求点D到平面BCE的距离。
如图,在四棱锥 中,底面
中,底面 为菱形,
为菱形, ,
, 为
为 的中点.
的中点.
(1)若 ,求证:平面
,求证:平面 平面
平面 ;
;
(2)设点 是线段
是线段 上的一点,
上的一点, ,且
,且 平面
平面 .
.
(1)求实数 的值;
的值;
(2)若 ,且平面
,且平面 平面
平面 ,求二面角
,求二面角 的大小.
的大小.
如图,三棱柱 中,侧棱
中,侧棱 垂直底面
垂直底面 ,底面三角形
,底面三角形 是正三角形,
是正三角形, 是
是 中点,则下列叙述正确的是( )
中点,则下列叙述正确的是( )

A. 与 与 是异面直线 是异面直线 |
B. 平面 平面 |
C. 与 与 为异面直线,且 为异面直线,且 |
D. 平面 平面 |
如图,在正方体 的棱长为
的棱长为 ,
, 为棱
为棱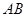 上的一动点.
上的一动点.

(1)若 为棱
为棱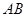 的中点,
的中点,
①求四棱锥 的体积
的体积
②求证:面 面
面
(2)若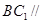 面
面 ,求证:
,求证: 为棱
为棱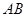 的中点.
的中点.
设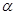 、
、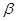 、
、 是三个不同的平面,
是三个不同的平面,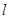 、
、 、
、 是三条不同的直线,则
是三条不同的直线,则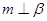 的一个充分条件为 .
的一个充分条件为 .
① ;
;
②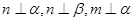 ;
;
③ ;
;
④ .
.