如图,等边三角形 的中线
的中线 与中位线
与中位线 相交于
相交于 ,已知
,已知 是△
是△ 绕
绕 旋转过程中的一个图形,下列命题中,错误的是()
旋转过程中的一个图形,下列命题中,错误的是()
A.动点 在平面 在平面 上的射影在线段 上的射影在线段 上 上 |
B.恒有平面 ⊥平面 ⊥平面 |
C.三棱锥 的体积有最大值 的体积有最大值 |
D.异面直线 与 与 不可能垂直 不可能垂直 |
如图, 是正方体
是正方体 对角线
对角线 上一动点,设
上一动点,设 的长度为
的长度为 ,若
,若 的面积为
的面积为 ,则
,则 的图象大致是()
的图象大致是()

在三棱锥 中,
中, ,G为
,G为 的重心,过点G作三棱锥的一个截面,使截面平行于直线PB和AC,则截面的周长为.
的重心,过点G作三棱锥的一个截面,使截面平行于直线PB和AC,则截面的周长为.
已知E、F、G、H分别是三棱锥A-BCD 棱AB、BC、CD、DA的中点,
(1)四边形EFGH是_______形
(2)AC与BD所成角为 ,且AC=BD=1,则EG=_______
,且AC=BD=1,则EG=_______
如右图,在长方体 中, ,一质点从顶点 射向点 ,遇长方体的面反射(反射服从光的反射原理),将 次到第 次反射点之间的线段记为 , ,将线段 竖直放置在同一水平线上,则大致的图形是()





A B C D
设△ABC的三边长分别为a、b、c,△ABC的面积为S,内切圆半径为r,则r= ;类比这个结论可知:四面体S-ABC的四个面的面积分别为S1、S2、S3、S4,内切球的半径为r,四面体S-ABC的体积为V,则r=( )
;类比这个结论可知:四面体S-ABC的四个面的面积分别为S1、S2、S3、S4,内切球的半径为r,四面体S-ABC的体积为V,则r=( )
A. |
B. |
C. |
D. |
如图,直三棱柱 中,
中,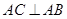 ,
, ,
,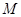 是
是 的中点,△
的中点,△ 是等腰三角形,
是等腰三角形, 为
为 的中点,
的中点,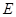 为
为 上一点.
上一点.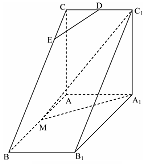
(1)若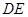 ∥平面
∥平面 ,求
,求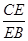 ;
;
(2)平面 将三棱柱
将三棱柱 分成两个部分,求较小部分与较大部分的体积之比.
分成两个部分,求较小部分与较大部分的体积之比.
如图,在四棱锥 中,底面
中,底面 为矩形,
为矩形, .
.
(1)求证 ,并指出异面直线PA与CD所成角的大小;
,并指出异面直线PA与CD所成角的大小;
(2)在棱 上是否存在一点
上是否存在一点 ,使得
,使得 ?如果存在,求出此时三棱锥
?如果存在,求出此时三棱锥 与四棱锥
与四棱锥 的体积比;如果不存在,请说明理由.
的体积比;如果不存在,请说明理由.
如图,四棱锥F-ABCD的底面ABCD是菱形,其对角线 AE、CF都与平面ABCD垂直,AE=1,CF=2.
AE、CF都与平面ABCD垂直,AE=1,CF=2.
(1)求二面角B-AF-D的大小;
(2)求四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积.
把四个半径都是1的球中的三个放在桌面上,使它两两外切,然后在它们上面放上第四个球,使它与前三个都相切,求第四个球的最高点与桌面的距离()
A. |
B. |
C. |
| D.3 |
如图,正方体 的棱长为
的棱长为 ,以顶点A为球心,2为半径作一个球,则图中球面与正方体的表面相交所得到的两段弧长之和等于( )
,以顶点A为球心,2为半径作一个球,则图中球面与正方体的表面相交所得到的两段弧长之和等于( )
A. |
B. |
C. |
D. |
设倒圆锥形容器的轴截面为一个等边三角形,在此容器内注入水,并浸入半径为 的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?
的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?