高中数学复合三角函数解答题

已知，
（1）求；
（2）在 (1) 的条件下，求的定义域和值域．

已知
求（1）和的值
（2）的值，并求的解析式。

已知函数，当时，有极大值；
（1）求的值；（2）求函数的极小值。

已知函数，．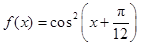
（1）设是函数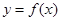的一个零点，求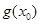的值；
（2）求函数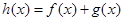的单调递增区间．

已知函数的图象经过点．
（Ⅰ）求的表达式及其导数；
（Ⅱ）求在闭区间上的最大值和最小值．

已知函数
（1）试求函数的最大值；
（2）若存在，使成立，试求的取值范围；
（3）当且时，不等式恒成立，求的取值范围；

本题满分16分）
设函数曲线在点处的切线方程为.
(1)求的解析式；
(2)证明：曲线上任一点处的切线与直线 及直线所围成的三角形的面积是一个定值,并求此定值.

若函数 $y=f\left(x\right)$在 $x=x_0$处取得极大值或极小值，则称 $x_0$为函数 $y=f\left(x\right)$的极值点.已知 $a,b$是实数，1和-1是函数 $f\left(x\right)=x^3+a{x}^2+bx$的两个极值点．
（1）求 $a$和 $b$的值；
（2）设函数 $g\left(x\right)$的导函数 $g`\left(x\right)=f\left(x\right)+2$，求 $g\left(x\right)$的极值点；
（3）设 $h\left(x\right)=f\left(f\right(x\left)\right)-c$，其中 $c\in [-2,2]$，求函数 $y=h\left(x\right)$的零点个数．

已知函数 $f\left(x\right)$满足满足 $f\left(x\right)=f`\left(1\right)e^{x-1}-f\left(0\right)x+\frac{1}{2}{x}^2$；
（1）求 $f\left(x\right)$的解析式及单调区间；
（2）若 $f\left(x\right)\ge \frac{1}{2}{x}^2+ax+b$，求 $(a+1)b$的最大值.

某花店每天以每枝 $5$元的价格从农场购进若干枝玫瑰花，然后以每枝 $10$元的价格出售，如果当天卖不完，剩下的玫瑰花作垃圾处理.
（1）若花店一天购进 $16$枝玫瑰花，求当天的利润 $y$(单位：元)关于当天需求量 $n$（单位：枝， $n\in N$）的函数解析式.
（2）花店记录了100天玫瑰花的日需求量（单位：枝），整理得下表：

以100天记录的各需求量的频率作为各需求量发生的概率.
（i）若花店一天购进 $16$枝玫瑰花， $X$表示当天的利润（单位：元），求 $X$的分布列，数学期望及方差；
（ii）若花店计划一天购进16枝或17枝玫瑰花，你认为应购进16枝还是17枝？请说明理由.

已知函数 $f\left(x\right)=a{x}^3+bx+c$在 $x=2$处取得极值为 $c-16$

（1）求 $a,b$的值；
（2）若 $f\left(x\right)$有极大值28，求 $f\left(x\right)$在 $[-3,3]$上的最大值．

定义在上的函数同时满足以下条件：
①在上是减函数，在上是增函数；②是偶函数；③在处的切线与直线垂直.
（1）求函数的解析式；
（2）设，若存在，使，求实数的取值范围.

把函数的图象按向量平移得到函数的图象．　
(1)求函数的解析式； (2)若，证明：.

已知函数f(x)(x∈R)满足f(x)＝，a≠0，f(1)＝1，且使f(x)＝2x成立的实数x只有一个．
(1)求函数f(x)的表达式；
(2)若数列{a_n}满足a₁＝，a_n+1＝f(a_n)，b_n＝－1，n∈N^*，证明数列{b_n}是等比数列，并求出{b_n}的通项公式；
(3)在(2)的条件下，证明：a₁b₁＋a₂b₂＋…＋a_nb_n<1(n∈N^*)．

若定义在R上的函数对任意的，都有
成立，且当时，．
(1)求的值；（2）求证：是R上的增函数；
(3) 若，不等式对任意的恒成立，求实数的取值范围．