已知函数f(x)(x∈R)满足f(x)＝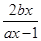
，a≠0，f(1)＝1，且使f(x)＝2x成立的实数x只有一个．
(1)求函数f(x)的表达式；
(2)若数列{an}满足a1＝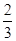
，an+1＝f(an)，bn＝
－1，n∈N*，证明数列{bn}是等比数列，并求出{bn}的通项公式；
(3)在(2)的条件下，证明：a1b1＋a2b2＋…＋anbn<1(n∈N*)．
相关试题
．
(
为自然对数的底数)时，求
的极小值；
零点的个数．
与
在第一象限内的交点为P．
且与曲线
相切的直线方程
；
所围图形的面积
．
处都取得极值．
的值；
的单调区间
在
上是单调增函数，则
的最大值是( )
，若存在互不相等的正整数
…
，使得
…
同时小于
，则记
为满足条件的
的最大值．
的值；
，
时，求
时，求相关知识点
推荐套卷
已知函数f(x)(x∈R)满足f(x)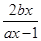＝，a≠0，f(1)＝1，且使f(x)＝2x成立的实数x只有一个．
(1)求函数f(x)的表达式；
(2)若数列{an}满足a1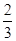＝，an+1＝f(an)，bn＝－1，n∈N*，证明数列{bn}是等比数列，并求出{bn}的通项公式；
(3)在(2)的条件下，证明：a1b1＋a2b2＋…＋anbn<1(n∈N*)．
粤公网安备 44130202000953号