高中数学复合三角函数解答题

已知：是一次函数，其图像过点，且，求的解析式。

已知函数的图象在与轴交点处的切线方程是.
(Ⅰ)求函数的解析式;
(Ⅱ)设函数,若的极值存在,求实数的取值范围以及当取何值时函数分别取得极大和极小值.

已知且，当时，恒有
求的解析式；
若的解集为空集，求的范围。

动点P从边长为1的正方形ABCD的顶点A出发顺次经过B、C、D，再回到A，设表示P点行程，表PA的长，求关于的函数关系式。

已知函数在点（1,f(1))处的切线方程为y = 2.
(I)求f(x)的解析式；
(II)设函数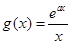若对任意的，总存唯一实数，使得,求实数a的取值范围.

已知函数=，数列满足，。
(1)求数列的通项公式；
(2)令-+-+…+-求；
(3)令=（，，+++┅，若<对一切都成立，求最小的正整数。

(本小题满分12分)已知函数满足.
（Ⅰ）求的解析式及其定义域；
（Ⅱ）写出的单调区间并证明.

（本小题满分12分）
已知令.
(1)求的表达式；
(2)若函数和函数的图象关于原点对称，
（ⅰ）求函数的解析式；
（ⅱ）若在区间上是增函数，求实数l的取值范围.

（本小题满分14分）
已知是定义在R上的奇函数，且，求：
（1）的解析式。
（2）已知，求函数在区间上的最小值。

（本题9分）函数是定义在上的奇函数，当时且。
（Ⅰ）求的值；
（Ⅱ）求的解析式。

(本题满分14分)已知函数的一系列对应值如下表：

（1）根据表格提供的数据求函数的解析式；
（2）根据（1）的结果，若函数周期为，求在区间上的最大、最小值及对应的的值.

若是定义在上的增函数，且对一切，满足.
（1）求的值；
（2）若，解不等式

已知函数，若在上的最大值为，求的解析式.

已知函数，若函数的图象上任意一点P关于原点的对称点Q的轨迹恰好是函数的图象：
（1）写出的解析式
（2）记，讨论的单调性
（3）若时，总有成立，求实数的取值范围。

（本小题满分12分）函数（）的最大值为1，对任意，有。
(1)求函数的解析式；
(2)若，其中，求的值。