高中数学随机事件解答题

改革开放以来，人们的支付方式发生了巨大转变．近年来，移动支付已成为主要支付方式之一．为了解某校学生上个月A，B两种移动支付方式的使用情况，从全校所有的1000名学生中随机抽取了100人，发现样本中A，B两种支付方式都不使用的有5人，样本中仅使用A和仅使用B的学生的支付金额分布情况如下：

支付金额 支付方式	不大于 $2000$ 元	大于 $2000$ 元
仅使用A	27人	3人
仅使用B	24人	1人

（Ⅰ）估计该校学生中上个月A，B两种支付方式都使用的人数；

（Ⅱ）从样本仅使用B的学生中随机抽取1人，求该学生上个月支付金额大于 $2000$ 元的概率；

（Ⅲ）已知上个月样本学生的支付方式在本月没有变化．现从样本仅使用B的学生中随机抽查1人，发现他本月的支付金额大于 $2000$ 元．结合（Ⅱ）的结果，能否认为样本仅使用B的学生中本月支付金额大于 $2000$ 元的人数有变化？说明理由．

某人去开会，他乘火车、轮船、汽车、飞机去的概率分别为0．3,0．2,0．1,0．4．
（1）求他乘火车或乘飞机去的概率；
（2）求他不乘飞机去的概率；
（3）若他去的概率为0．5，请问他有可能是乘何种交通工具去的？

某学校共有教职工900人，分成三个批次进行继续教育培训，在三个批次中男、女教职工人数如下表所示．已知在全体教职工中随机抽取1名，抽到第二批次中女教职工的概率是0．16 ．

	第一批	第二批	第三批
女	196	x	y
男	204	156	z

 
（1）求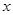的值；
（2）现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查，问应在第三批次中抽取教职工多少名？
（3）已知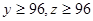，求第三批次中女教职工比男教职工多的概率．

某食品企业一个月内被消费者投诉的次数用ξ表示，椐统计，随机变量ξ的概率分布如下：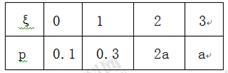

（Ⅰ）求a的值和ξ的数学期望；
（Ⅱ）假设一月份与二月份被消费者投诉的次数互不影响，求该企业在这两个月内共被消费者投诉2次的概率．

(本题14分)张老师居住在某城镇的A处，准备开车到学校B处上班。若该地各路段发生堵车事件都是独立的，且在同一路段发生堵车事件最多只有一次，发生堵车事件的概率如图。（例如：A→C→D算作两个路段：路段AC发生堵车事件的概率为，路段CD发生堵车事件的概率为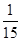）。（1）请你为其选择一条由A到B的路线，使得途中发生堵车事件的概率最小；（2）若记路线A→C→F→B中遇到堵车次数为随机变量，求的数学期望。

某射手进行射击训练，假设每次射击击中目标的概率为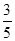，且每次射击的结果互不影响，已知射手射击了5
次，求：
(1)其中只在第一、三、五次击中目标的概率；
(2)其中恰有3次击中目标的概率．

为了解某校学生的视力情况，现采用随机抽样的方式从该校的A，B两班中各抽5名学生进行视力检测．检测的数据如下：
A班5名学生的视力检测结果：4.3，5.1，4.6，4.1，4.9.
B班5名学生的视力检测结果：5.1，4.9，4.0，4.0，4.5.
（1）分别计算两组数据的平均数，从计算结果看，哪个班的学生视力较好？；
（2）由数据判断哪个班的5名学生视力方差较大？（结论不要求证明）
（3）根据数据推断A班全班40名学生中有几名学生的视力大于4.6？

小王参加一次比赛，比赛共设三关，第一、二关各有两个必答题，如果每关两个问题都答对，可进入下一关，第三关有三个问题，只要答对其中两个问题，则闯关成功．每过一关可一次性获得价值分别为1000元，3000元，6000元的奖品(不重复得奖)，小王对三关中每个问题回答正确的概率依次为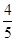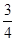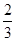，，，且每个问题回答正确与否相互独立．
(1)求小王过第一关但未过第二关的概率；
(2)用X表示小王所获得奖品的价值，写出X的概率分布列，并求X的数学期望．

一个盒子里装有三张卡片，分别标记有数字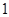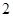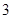，，，这三张卡片除标记的数字外完全相同。随机有放回地抽取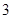次，每次抽取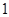张，将抽取的卡片上的数字依次记为.
（Ⅰ）求"抽取的卡片上的数字满足"的概率；
（Ⅱ）求"抽取的卡片上的数字不完全相同"的概率.

已知箱子里装有4张大小、形状都相同的卡片，标号分别为1,2,3,4．
（1）从箱子中任取两张卡片，求两张卡片的标号之和不小于5的概率；
（2）从箱子中任意取出一张卡片，记下它的标号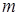，然后再放回箱子中；第二次再从箱子中任取一张卡片，记下它的标号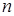，求使得幂函数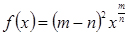图像关于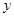轴对称的概率．

某校在教师外出培训学习活动中,在一个月派出的培训人数及其概率如下表所示：

派出人数	2人及以下	3	4	5	6人及以上
概率	0.1	0.46	0.3	0.1	0.04

 
⑴求有4个人或5个人培训的概率；
⑵求至少有3个人培训的概率.

某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，其可见部分如下，据此解答如下问题：
 
（1）计算频率分布直方图中[80,90)间的矩形的高；
（2）若要从分数在之间的试卷中任取两份分析学生失分情况，求在抽取的试卷中，至少有一份的分数在之间的概率；
（3）根据频率分布直方图估计这次测试的平均分．

“根据《中华人民共和国道路交通安全法》规定：车辆驾驶员血液酒精浓度在20～80 mg/100ml（不含80）之间，属于酒后驾车，血液酒精浓度在80mg/100ml（含80）以上时，属醉酒驾车．”某市交警在该市一交通岗前设点对过往的车辆进行抽查，经过一晚的抽查，共查出酒后驾车者60名，图甲是用酒精测试仪对这60 名酒后驾车者血液中酒精浓度进行检测后依所得结果画出的频率分布直方图．

（1）统计方法中，同一组数据常用该组区间的中点值作为代表，图乙的程序框图是对这60名酒后驾车者血液的酒精浓度做进一步的统计，求出图乙输出的S的值，并说明S的统计意义；（图乙中数据与分别表示图甲中各组的组中值及频率）

（2）本次行动中，吴、李两位先生都被酒精测试仪测得酒精浓度属于70～90的范围，但他俩坚称没喝那么多，是测试仪不准，交警大队队长决定在被酒精测试仪测得酒精浓度属于70～90范围的酒后驾车者中随机抽出2人抽血检验，设为吴、李两位先生被抽中的人数，求的分布列，并求吴、李两位先生至少有1人被抽中的概率；

为了解某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：

	喜爱打篮球	不喜爱打篮球	合计
男生		5
女生	10
合计			50

已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为．
（1）请将上面的列联表补充完整；
（2）是否有99.5％的把握认为喜爱打篮球与性别有关？说明你的理由；
（3）已知喜爱打篮球的10位女生中，还喜欢打羽毛球，还喜欢打乒乓球，还喜欢踢足球，现在从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查，求和不全被选中的概率．
下面的临界值表供参考：

	0.15	0.10	0.05	0.025	0.010	0.005	0.001
	2.072	2.706	3.841	5.024	6.635	7.879	10.828

（参考公式：）

（本小题满分12分）
某家电生产企业市场营销部对本厂生产的某种电器进行了市场调查，发现每台的销售利润与该电器的无故障使用时间（单位：年）有关．若，则销售利润为元；若，则销售利润为元；若，则销售利润为元，设每台该种电器的无故障使用时间，，这三种情况发生的概率分别是，又知是方程的两个根，且．
（1）求的值；
（2）记表示销售两台该种电器的销售利润总和，求的分布列及期望．