第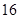 届亚运会于
届亚运会于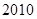 年
年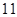 月
月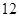 日至
日至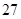 日在中国广州进行,为了做好接待工作,组委会招募了
日在中国广州进行,为了做好接待工作,组委会招募了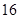 名男志愿者和
名男志愿者和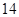 名女志愿者,调查发现,男、女志愿者中分别有
名女志愿者,调查发现,男、女志愿者中分别有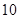 人和
人和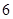 人喜爱运动,其余不喜爱.
人喜爱运动,其余不喜爱.
(1)根据以上数据完成以下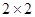 列联表:
列联表:
| |
喜爱运动 |
不喜爱运动 |
总计 |
| 男 |
10 |
|
16 |
| 女 |
6 |
|
14 |
| 总计 |
|
|
30 |
(2)能否在犯错误的概率不超过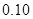 的前提下认为性别与喜爱运动有关?
的前提下认为性别与喜爱运动有关?
(3)如果从喜欢运动的女志愿者中(其中恰有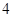 人会外语),抽取
人会外语),抽取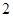 名负责翻译工作,则抽出的志愿者中
名负责翻译工作,则抽出的志愿者中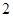 人都能胜任翻译工作的概率是多少?
人都能胜任翻译工作的概率是多少?
附:K2=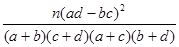
| P(K2≥k) |
0.100 |
0.050 |
0.025 |
0.010 |
0.001 |
| k |
2.706 |
3.841 |
5.024 |
6.635 |
10.828 |
下表提供了某厂节能降耗技术发行后,生产甲产品过程中记录的产量 (吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
(1)求线性回归方程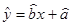 所表示的直线必经过的点;
所表示的直线必经过的点;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程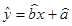 ;
;
并预测生产1000吨甲产品的生产能耗多少吨标准煤?
(参考: )
)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨
标准煤)的几组对照数据:
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产
l00吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5="66.5"
用最小二乘法求线性回归方程系数公式 ).
).
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2的列联表;
(2)判断性别与休闲方式是否有关系。
附:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
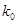 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量
(吨)与相应的生产能耗
(吨标准煤)的几组对照数据
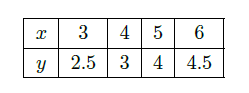
(1) 请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出
关于
的线性回归方程
;
(3)已知该厂技术改造前
吨甲产品能耗为
吨标准煤.试根据(2)求出的线性回归方程,预测生产
吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考数据:
)
(本小题满分 12分
12分 )
)
在对人们休闲方式的一次调查中,共调查120人,其中女性70人、男性50人,女性中有40人主要的休闲方式是看电视,另外30人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外30人主要的休闲方式是运动。 (I)根据以上数据建立一个2×2的列联表:
(I)根据以上数据建立一个2×2的列联表:
| 休闲方式 性别 |
看电视 |
运动 |
总计 |
| 女性 |
|
|
|
| 男性 |
|
|
|
| 总计 |
|
|
|
(II)休闲方式与性别是否有关?

随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如下图 .
⑴根据茎叶图判断哪个班的平均身高较高;
⑵计算甲班的样本方差.
本题满分12分)某农科所对冬季昼夜温差与某反季节大豆种子发芽多少之间的关系进行分析研究,他们记录了12月1日至5日的昼夜温差与每天100颗种子的发芽数,数据如下表:
| 日 期 |
12月1日 |
12月2日 |
12月3日 |
12月4日 |
12月5日 |
温差 (0C) (0C) |
10 |
11 |
13 |
12 |
8 |
发芽数 (颗) (颗) |
23 |
25 |
30 |
26 |
16 |
该农科所确定的研究方案是:先从五组数据中选取两组,用剩下的3组数据求线性回归方程,再用被选取的两组数据进行检验.
(1) 若先选取的是12月1日和5日的数据,请根据2日至4日的三组数据,求 关于
关于 的线性回归方程
的线性回归方程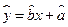 ;
;
(2) 若由回归方程得到的估计数据与检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试判断(1)中所得的线性回归方程是否可靠?说明理由.
(本小题12分)
某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据
| x |
6 |
8 |
10 |
12 |
| y |
2 |
3 |
5 |
6 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ;
;
(3)试根据(II)求出的线性回归方程,预测记忆力为9的同学的判断力。
(相关公式: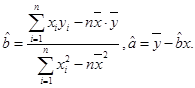 )
)
(本小题满分10分)
从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭7次,命中的环数如下:
| 甲 |
10 |
8 |
6 |
9 |
7 |
6 |
10 |
| 乙 |
10 |
9 |
8 |
6 |
7 |
8 |
8 |
(1)计算甲、乙两人射箭命中环数的平均数和方差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.
(本小题满分14分)已知x,y之间的一组数据如下表:
| x |
1 |
3 |
6 |
7 |
8 |
| y |
1 |
2 |
3 |
4 |
5 |
(1)以x为横坐标,y为纵坐标在直角坐标系中画出散点图,并说明这两个变量之间的关系是正相关关系还是负相关关系。
(2)求线性回归方程.
一次考试中,五名学生的数学、物理成绩如下表所示:
| 学生 |
A1 |
A2 |
A3 |
A4 |
A5 |
| 数学(x分 |
89 |
91 |
93 |
95 |
97 |
| 物理(y分) |
87 |
89 |
89 |
92 |
93 |
(1)请在图的直角坐标系中作出这些数据的散点图,并求出这些数据的同归方程;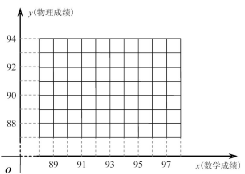
(2)要从4名数学成绩在90分以上的同学中选2人参加一项活动,以X表示选中的同学的物理成绩高于90分的人数,求随机变量X的分布列及数学期望E(X)的值.
某研究小组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试的成绩(百分制)如下表所示:
| 序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 数学成绩 |
95 |
75 |
80 |
94 |
92 |
65 |
67 |
84 |
98 |
71 |
| 物理成绩 |
90 |
63 |
72 |
87 |
91 |
71 |
58 |
82 |
93 |
80 |
| 序号 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| 数学成绩 |
67 |
93 |
64 |
78 |
77 |
90 |
57 |
84 |
72 |
83 |
| 物理成绩 |
77 |
82 |
48 |
85 |
69 |
91 |
61 |
82 |
78 |
86 |
若数学成绩90分(含90分)以上为优秀,物理成绩85分(含85分)以上为优秀。
⑴根据上表完成下面的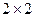 列联表:
列联表:
| |
数学成绩优秀 |
数学成绩不优秀 |
合计 |
| 物理成绩优秀 |
|
|
|
| 物理成绩不优秀 |
|
12 |
|
| 合计 |
|
|
20 |
⑵根据⑴中表格的数据计算,有多少的把握,认为学生的数学成绩与物理成绩之间有关系?
某工厂在2004年的各月中,一产品的月总成本y(万元)与月产量x(吨)之间有如下数据:
| X |
4.16 |
4.24 |
4.38 |
4.56 |
4.72 |
4.96 |
5.18 |
5.36 |
5.6 |
5.74 |
5.96 |
6.14 |
| Y |
4.38 |
4.56 |
4.6 |
4.83 |
4.96 |
5.13 |
5.38 |
5.55 |
5.71 |
5.89 |
6.04 |
6.25 |
若2005年1月份该产品的计划产量是6吨,试估计该产品1月份的总成本.