[广东]2013届广东省深圳市高三第一次调研考试理科数学试卷
化简sin 2013o的结果是
| A.sin 33o | B.cos33o | C.-sin 33o | D.-cos33o |
图是一个几何体的三视图,根据图中数据,可得该几何体的表面积、体积分别是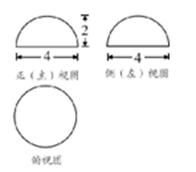
A.32 、 、 |
B.16 、 、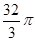 |
C.12 、 、 |
D.8 、 、 |
等差数列{an}中,a1,a2,a3分别是下表第一、二、三行中的某一个数,且a1,a2,a3中的任何两个数不在下表的同一列。
| |
第一列 |
第二列 |
第三列 |
| 第一行 |
2 |
3 |
5 |
| 第二行 |
8 |
6 |
14 |
| 第三行 |
11 |
9 |
13 |
则a4的值为
A.18 B.15 C.12 D.20
我们把各位数字之和为6的四位数称为“六合数”(如2013是“六合数”),则“六合数”中首位为2的“六合数”共有
| A.18个 | B.15个 | C.12个 | D.9个 |
函数y = 1n|x-1|的图像与函数y="-2" cos  x(-2≤x≤4)的图像所有交点的横坐标之和等于
x(-2≤x≤4)的图像所有交点的横坐标之和等于
| A.8 | B.6 | C.4 | D.2 |
函数y=f(x),x∈D,若存在常数C,对任意的xl∈D,仔在唯一的x2∈D,使得  ,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为
,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为
A. B.2 C.4 D. 2
B.2 C.4 D. 2
容量为60的样本的频率分布直方图共有n(n>1)个小矩形,若其中一个小矩形的面积等于其余n-1个小矩形面积和的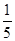 ,则这个小矩形对应的频数是____ .
,则这个小矩形对应的频数是____ .
已知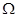 = {(x,y)|x+ y≤6,x≥0,y≥0},A={(x,y)|x≤4,y>0,x-y2≥0},若向区域
= {(x,y)|x+ y≤6,x≥0,y≥0},A={(x,y)|x≤4,y>0,x-y2≥0},若向区域 上随机投一点P,则点P落入区域A的概率是 .
上随机投一点P,则点P落入区域A的概率是 .
若执行图中的框图,输入N=13,则输出的数等于 。(注:“S=0”,即为“S←0”或为“S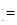 0”.)
0”.)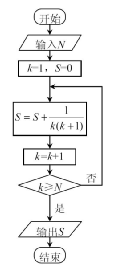
设集合A={(x,y)|(x一4)2+y2=1},B={(x,y)|(x-t)2+(y-at+ 2)2=l},如果命题“ ∈R,
∈R, ”是真命题,则实数a的取值范围是 。
”是真命题,则实数a的取值范围是 。
在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.曲线C1的参数方程为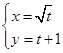 (t为参数),曲线C2的极坐标方程为
(t为参数),曲线C2的极坐标方程为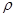 sin
sin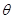 -
-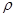 cos
cos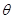 =3,则Cl与C2交点在直角坐标系中的坐标为 。
=3,则Cl与C2交点在直角坐标系中的坐标为 。
如图3,在⊙O中,直径AB与弦CD垂直,垂足为E,EF⊥BC,垂足为F,若AB=6,CF·CB=5,则AE= 。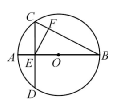
已知函数f(x)="2" sin (0≤x≤5),点A、B分别是函数y=f(x)图像上的最高点和最低点.
(0≤x≤5),点A、B分别是函数y=f(x)图像上的最高点和最低点.
(1)求点A、B的坐标以及 ·
· 的值;
的值;
(2)没点A、B分别在角 、
、 的终边上,求tan(
的终边上,求tan( )的值.
)的值.
一次考试中,五名学生的数学、物理成绩如下表所示:
| 学生 |
A1 |
A2 |
A3 |
A4 |
A5 |
| 数学(x分 |
89 |
91 |
93 |
95 |
97 |
| 物理(y分) |
87 |
89 |
89 |
92 |
93 |
(1)请在图的直角坐标系中作出这些数据的散点图,并求出这些数据的同归方程;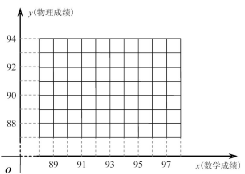
(2)要从4名数学成绩在90分以上的同学中选2人参加一项活动,以X表示选中的同学的物理成绩高于90分的人数,求随机变量X的分布列及数学期望E(X)的值.
如图,⊙O的直径AB=4,点C、D为⊙O上两点,且∠CA B=45o,∠DAB=60o,F为 的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图).
的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图).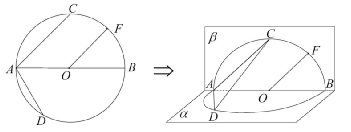
(1)求证:OF//平面ACD;
(2)求二面角C- AD-B的余弦值;
(3)在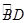 上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置,并求直线AG与平面ACD所成角的正弦值;若不存在,请说明理由.
上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置,并求直线AG与平面ACD所成角的正弦值;若不存在,请说明理由.
已知数列{an}满足:a1=1,a2=(a≠0),an+2=p· (其中P为非零常数,n∈N *)
(其中P为非零常数,n∈N *)
(1)判断数列{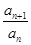 }是不是等比数列?
}是不是等比数列?
(2)求an;
(3)当a=1时,令bn=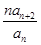 ,Sn为数列{bn}的前n项和,求Sn。
,Sn为数列{bn}的前n项和,求Sn。
已知两点F1(-1,0)及F2(1,0),点P在以F1、F2为焦点的椭圆C上,且|PF1|、|F1F2|、|PF2|构成等差数列.
(1)求椭圆C的方程;
(2)如图,动直线l:y=kx+m与椭圆C有且仅有一个公共点,点M,N是直线l上的两点,且F1M⊥l,F2N⊥l.求四边形F1MNF2面积S的最大值.
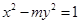 的实轴长是虚轴长的2倍,则rn=
的实轴长是虚轴长的2倍,则rn=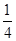
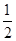
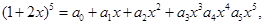 则a3= 。
则a3= 。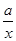 (a>0),g(x)=2lnx+bx且直线y=2x-2与曲线y=g(x)相切.
(a>0),g(x)=2lnx+bx且直线y=2x-2与曲线y=g(x)相切. )内的一切实数x,小等式f(x)≥g(x)恒成立,求实数a的取值范围;
)内的一切实数x,小等式f(x)≥g(x)恒成立,求实数a的取值范围; 成立;
成立; .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号