已知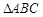 的三内角分别为
的三内角分别为 ,向量
,向量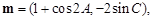
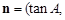
 ,记函数
,记函数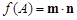 .
.
(1)若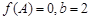 ,求
,求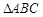 的面积;
的面积;
(2)若关于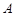 的方程
的方程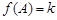 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围.
已知A、B、C、P为平面内四点,求证:A、B、C三点在一条直线上的充要条件是存在一对实数m、n,使 =m
=m +n
+n ,且m+n=1.
,且m+n=1.
已知 的三个内角A、B、C所对的三边分别是a、b、c,平面向量
的三个内角A、B、C所对的三边分别是a、b、c,平面向量 ,平面向量
,平面向量
(I)如果 求a的值;
求a的值;
(II)若 请判断
请判断 的形状.
的形状.
(本题满分15分)已知向量 ,
,
(1)若 ,求实数
,求实数 的值;
的值;
(2)若 ,求实数
,求实数 的值;
的值;
(3)若 ,且存在不等于零的实数
,且存在不等于零的实数 使得
使得 ,试求
,试求 的最小值.
的最小值.
(已知 是平面内两个不共线的非零向量,
是平面内两个不共线的非零向量, ,
, ,
, ,且
,且 三点共线.
三点共线.
(1)求实数 的值;
的值;
(2)若 ,
, ,求
,求 的坐标;
的坐标;
(3)已知点 ,在(2)的条件下,若
,在(2)的条件下,若 四点按逆时针顺序构成平行四边形, 求点A的坐标.
四点按逆时针顺序构成平行四边形, 求点A的坐标.