关于函数 ,看下面四个结论:
,看下面四个结论:
① 是奇函数;
是奇函数;
②当 时,
时, 恒成立;
恒成立;
③ 的最大值是
的最大值是 ;
;
④ 的最小值是
的最小值是 .
.
其中正确结论的个数为()
| A.1个 | B.2个 | C.3个 | D.4个 |
对任意的实数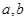 ,记
,记 ,若
,若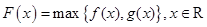 ,其中奇函数
,其中奇函数 在
在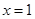 时有极小值-2,
时有极小值-2,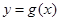 是正比例函数,函数
是正比例函数,函数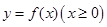 与函数
与函数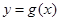 的图象如图所示.则下列关于函数
的图象如图所示.则下列关于函数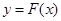 的说法中,正确的是()
的说法中,正确的是()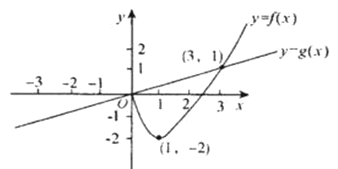
A.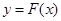 为奇函数 为奇函数 |
B.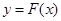 在 在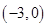 为增函数 为增函数 |
C.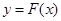 有极大值 有极大值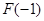 ,极小值 ,极小值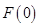 |
D.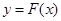 最小值为-2,最大值为2 最小值为-2,最大值为2 |
设x∈R,对于使﹣x2+2x≤M成立的所有常数M中,我们把M的最小值1叫做﹣x2+2x的上确界.若a,b∈R+,且a+b=1,则 的上确界为()
的上确界为()
| A.﹣5 | B.﹣4 | C. |
D. |
给出定义:若  (其中
(其中 为整数),则
为整数),则 叫做离实数
叫做离实数 最近的整数,记作
最近的整数,记作 ,即
,即 .在此基础上给出下列关于函数
.在此基础上给出下列关于函数 的四个命题:
的四个命题:
①函数 的定义域是
的定义域是 ,值域是
,值域是 ;
;
②函数 的图像关于
的图像关于 轴对称;
轴对称;
③函数 的图像关于坐标原点对称;
的图像关于坐标原点对称;
④函数 在
在 上是增函数;
上是增函数;
则其中正确命题的个数是().
| A.1 | B.2 | C.3 | D.4 |