已知偶函数f(x)在区间[0,+∞)单调递减,则满足f(lnx)>f(1)的x取值范围是()
A.( ,1) ,1) |
B.(0, )∪(1,+∞) )∪(1,+∞) |
C.( ,e) ,e) |
| D.(0,1)∪(e,+∞) |
函数y=ax2+bx+3在(-∞,-1]上是增函数,在[-1,+∞)上是减函数,则()
| A.b>0且a<0 | B.b=2a<0 | C.b=2a>0 | D.a,b的符号不定 |
已知f(x)=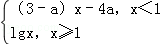 是(﹣∞,+∞)上的增函数,那么a的取值范围是()
是(﹣∞,+∞)上的增函数,那么a的取值范围是()
| A.(1,+∞) | B.(﹣∞,3) |
C.[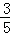 ,3) ,3) |
D.(1,3) |
若偶函数f(x)在(-∞,-1]上是增函数,则下列关系式中,成立的是()
A. <f(-1)<f(2) <f(-1)<f(2) |
B.f(-1)< <f(2) <f(2) |
C.f(2)<f(-1)< |
D.f(2)< <f(-1) <f(-1) |
已知函数f(x)=x3+ax2﹣9x+1,下列结论中错误的是()
A. x0∈R,f(x0)=0 x0∈R,f(x0)=0 |
| B.“a=3”是“﹣3为f(x)的极大值点”的充分不必要条件 |
| C.若x0是f(x)的极小值点,则f(x)在区间(x0,+∞)单调递增 |
| D.若3是f(x)的极值点,则f(x)的单调递减区间是(﹣1,3) |