设函数
 ,集合
,集合 其中
其中
 <
< ,则使
,则使 成立的实数对
成立的实数对 有( )
有( )
| A.0个 | B.1个 | C.2个 | D.无数多个 |
若函数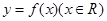 满足
满足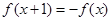 且
且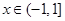 时,
时,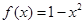 ,函数
,函数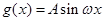 分别在两相邻对称轴
分别在两相邻对称轴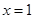 与
与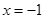 处取得最值1与-1,则函数
处取得最值1与-1,则函数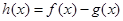 在区间
在区间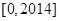 内零点的个数为()
内零点的个数为()
| A.1006 | B.1007 | C.1008 | D.1010 |
已知函数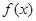 和
和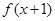 都是定义在R上的偶函数,若
都是定义在R上的偶函数,若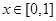 时,
时,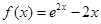 ,则
,则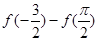 为()
为()
| A.正数 | B.负数 | C.零 | D.不能确定 |
已知函数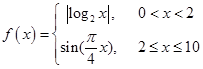 ,若存在实数
,若存在实数 满足
满足 ,且
,且 ,则
,则 的取值范围()
的取值范围()
| A.(20,32) | B.(9,21) | C.(8,24) | D.(15,25) |
现有四个函数① ②
② ,③
,③ ,④
,④ 的部分图象如下,但顺序被打乱,则按照图象从左到右的顺序,对应的函数序号正确的一组是( )
的部分图象如下,但顺序被打乱,则按照图象从左到右的顺序,对应的函数序号正确的一组是( )
| A.①④②③ | B.①④③② | C.④①②③ | D.③④②① |
设函数
 ,集合
,集合 其中
其中
 <
< ,则使
,则使 成立的实数对
成立的实数对 有
有
| A.0个 | B.1个 | C.2个 | D.无数多个 |
对非零实数 ,定义运算
,定义运算 满足:(1)
满足:(1) ; (2)
; (2)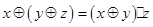 .若
.若 ,则下列判断正确的是( )
,则下列判断正确的是( )
A.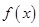 是增函数又是奇函数 是增函数又是奇函数 |
B.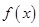 是减函数又是奇函数 是减函数又是奇函数 |
C.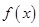 是增函数又是偶函数 是增函数又是偶函数 |
D.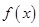 是减函数又是偶函数 是减函数又是偶函数 |
已知函数f(x)= 单调递减,那么实数a的取值范围是( )
单调递减,那么实数a的取值范围是( )
| A.(0,1) | B.(0, ) ) |
C.[ , , ) ) |
D.[ ,1) ,1) |
设奇函数f(x)在[-1,1]上是增函数,且f(-1)=-1,若函数f(x)≤t2-2at+1对所有的x∈[-1,1]都成立,则当a∈[-1,1]时t的取值范围是( )
| A.-2≤t≤2 | B.- ≤t≤ ≤t≤ |
| C.t≤-2或t=0或t≥2 | D.t≤- 或t=0或t≥ 或t=0或t≥ |
已知函数f(x)是R上的单调递增函数且为奇函数,数列{an}是等差数列,a3>0,则f(a1)+f(a3)+f(a5)的值( )
| A.恒为正数 |
| B.恒为负数 |
| C.恒为0 |
| D.可以为正数也可以为负数 |
已知f(x)是定义在(0,+∞) 上的非负可导函数,且满足xf′(x)+f(x)≤0,对任意的0<a<b,则必有( ).
| A.af(b)≤bf(a) | B.bf(a)≤af(b) |
| C.af(a)≤f(b) | D.bf(b)≤f(a) |