从数列 中抽出一些项,依原来的顺序组成的新数列叫数列
中抽出一些项,依原来的顺序组成的新数列叫数列 的一个子列.
的一个子列.
(1)写出数列 的一个是等比数列的子列;
的一个是等比数列的子列;
(2)设 是无穷等比数列,首项
是无穷等比数列,首项 ,公比为
,公比为 .求证:当
.求证:当 时,数列
时,数列 不存在
不存在
是无穷等差数列的子列.
如图,四边形ABCD与四边形 都为正方形,
都为正方形,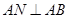 ,F
,F
为线段 的中点,E为线段BC上的动点.
的中点,E为线段BC上的动点.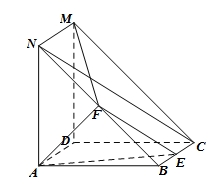
(1)当E为线段BC中点时,求证: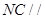 平面AEF;
平面AEF;
(2)求证:平面AEF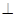
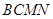 平面;
平面;
(3)设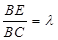 ,写出
,写出 为何值时MF⊥平面AEF(结论不要求证明).
为何值时MF⊥平面AEF(结论不要求证明).
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱AB上的动点.
(1)求证:DA1⊥ED1;
(2)若直线DA1与平面CED1成角为45o,求 的值;
的值;
(3)写出点E到直线D1C距离的最大值及此时点E的位置(结论不要求证明).
对于两个图形 ,我们将图形
,我们将图形 上的任意一点与图形
上的任意一点与图形 上的任意一点间的距离中的最小值,叫做图形
上的任意一点间的距离中的最小值,叫做图形 与图形
与图形 的距离.若两个函数图像的距离小于1,陈这两个函数互为“可及函数”.给出下列几对函数,其中互为“可及函数”的是_________.(写出所有正确命题的编号).
的距离.若两个函数图像的距离小于1,陈这两个函数互为“可及函数”.给出下列几对函数,其中互为“可及函数”的是_________.(写出所有正确命题的编号).
① ;
;
② ,
, ;
;
③ ,
, ;
;
④ ,
, ;
;
⑤ ,
, .
.
 中,角
中,角 所对的边分别为
所对的边分别为 ,下列命题正确的是________(写出正确命题的编号).
,下列命题正确的是________(写出正确命题的编号).
①总存在某内角 ,使
,使 ;
;
②若 ,则
,则 ;
;
③存在某钝角 ,有
,有 ;
;
④若 ,则
,则 的最小角小于
的最小角小于 ;
;
⑤若 ,则
,则 .
.
已知正方体 中,线段
中,线段 上(不包括端点)各有一点
上(不包括端点)各有一点 ,且
,且 ,下列说法中,不正确的是( )
,下列说法中,不正确的是( ) 四点共面
四点共面
B.直线 与平面
与平面 所成的角为定值
所成的角为定值
C.
D.设二面角 的大小为
的大小为 ,则
,则 的最小值为
的最小值为
在正项数列 中,
中, .对任意的
.对任意的 ,函数
,函数


 满足
满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 .
.
如图, 是以
是以 为直径的半圆
为直径的半圆 上异于
上异于 、
、 的点,矩形
的点,矩形 所在的平面垂直于半圆
所在的平面垂直于半圆 所在的平面,且
所在的平面,且 .
.
(1)求证: ;
;
(2)若异面直线 和
和 所成的角为
所成的角为 ,求平面
,求平面 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
已知函数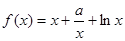 ,(
,(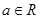 ).
).
(1)若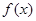 有最值,求实数
有最值,求实数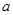 的取值范围;
的取值范围;
(2)当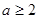 时,若存在
时,若存在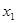 、
、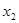
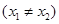 ,使得曲线
,使得曲线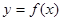 在
在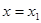 与
与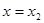 处的切线互相平行,求证:
处的切线互相平行,求证: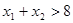 .
.
已知离心率为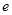 的双曲线和离心率为
的双曲线和离心率为 的椭圆有相同的焦点
的椭圆有相同的焦点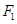 、
、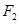 ,
,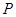 是两曲线的一个公共点,若
是两曲线的一个公共点,若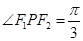 ,则
,则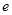 等于( )
等于( )
A.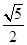 |
B.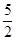 |
C.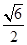 |
D.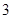 |
如图,半径为30 的圆形(
的圆形( 为圆心)铁皮上截取一块矩形材料
为圆心)铁皮上截取一块矩形材料 ,其中点
,其中点 在圆弧上,点
在圆弧上,点 在两半径上,现将此矩形材料卷成一个以
在两半径上,现将此矩形材料卷成一个以 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设 与矩形材料的边
与矩形材料的边 的夹角为
的夹角为 ,圆柱的体积为
,圆柱的体积为
 .
.
(1)求 关于
关于 的函数关系式?
的函数关系式?
(2)求圆柱形罐子体积 的最大值.
的最大值.
已知数列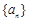 的前
的前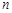 项和为
项和为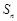 满足
满足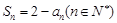 .
.
(1)求数列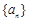 的通项公式;
的通项公式;
(2)求数列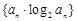 的前
的前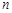 项和
项和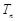 .
.
如图,在四棱锥 中,底面
中,底面 为直角梯形,且
为直角梯形,且 ,
, ,平面
,平面 底面
底面 ,
, 为
为 的中点,
的中点, 是棱
是棱 的中点,
的中点, .
.
(1)求证: 平面
平面 ;
;
(2)求三棱锥 的体积.
的体积.
已知函数 ,钝角
,钝角 (角
(角 对边为
对边为 )的角
)的角 满足
满足 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)若 ,求
,求 .
.