已知椭圆 的离心率为
的离心率为 ,以原点为圆心,椭圆短半轴长为半径的圆与直线
,以原点为圆心,椭圆短半轴长为半径的圆与直线 相切.
相切.
(1)求椭圆 的标准方程;
的标准方程;
(2)过右焦点 作斜率为
作斜率为 的直线
的直线 交曲线
交曲线 于
于 、
、 两点,且
两点,且 ,又点
,又点 关于原点
关于原点 的对称点为点
的对称点为点 ,试问
,试问 、
、 、
、 、
、 四点是否共圆?若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
四点是否共圆?若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
如图,已知长方形 中,
中, ,
, 为
为 的中点.将
的中点.将 沿
沿 折起,使得平面
折起,使得平面 平面
平面 .
.

(1)求证: ;
;
(2)若点 是线段
是线段 上的一动点,问点E在何位置时,二面角
上的一动点,问点E在何位置时,二面角 的余弦值为
的余弦值为 .
.
已知抛物线 的焦点为
的焦点为 ,点
,点 为抛物线上的一点,其纵坐标为
为抛物线上的一点,其纵坐标为 ,
, .
.
(1)求抛物线的方程;
(2)设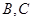 为抛物线上不同于
为抛物线上不同于 的两点,且
的两点,且 ,过
,过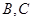 两点分别作抛物线的切线,记两切线的交点为
两点分别作抛物线的切线,记两切线的交点为 ,求
,求 的最小值.
的最小值.
在 中,角
中,角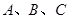 所对的边分别为
所对的边分别为 ,
,
向量

 ),且
),且 .
.
(1)求角 的大小;
的大小;
(2)若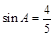 ,求
,求 的值.
的值.
已知直线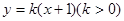 与函数
与函数 的图象恰有四个公共点
的图象恰有四个公共点 ,
, ,
, ,
, 其中
其中 ,则有( )
,则有( )
A. |
B. |
C. |
D.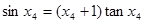 |
双曲线 的左、右焦点分别为
的左、右焦点分别为 ,若
,若 为其上一点,且
为其上一点,且 ,
, ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A. |
B. |
C. |
D. |
已知平面直角坐标系 ,以
,以 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系,,曲线
轴的非负半轴为极轴建立极坐标系,,曲线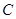 的参数方程为
的参数方程为 .点
.点 是曲线
是曲线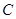 上两点,点
上两点,点 的极坐标分别为
的极坐标分别为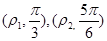 .
.
(1)写出曲线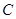 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)求 的值.
的值.
已知,函数 .
.
(1)如果 时,
时, 恒成立,求m的取值范围;
恒成立,求m的取值范围;
(2)当 时,求证:
时,求证: .
.
已知点 点
点 分别是
分别是 轴和
轴和 轴上的动点,且
轴上的动点,且 ,动点
,动点 满足
满足 ,设动点
,设动点 的轨迹为E.
的轨迹为E.
(1)求曲线E的方程;
(2)点Q(1,a),M,N为曲线E上不同的三点,且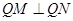 ,过M,N两点分别作曲线E的切线,记两切线的交点为
,过M,N两点分别作曲线E的切线,记两切线的交点为 ,求
,求 的最小值.
的最小值.
如图,在斜三棱柱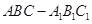 中,侧面
中,侧面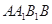 ⊥底面
⊥底面 ,侧棱
,侧棱 与底面
与底面 成60°的角,
成60°的角, .底面
.底面 是边长为2的正三角形,其重心为
是边长为2的正三角形,其重心为 点,
点, 是线段
是线段 上一点,且
上一点,且 .
.
(1)求证: //侧面
//侧面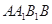 ;
;
(2)求平面 与底面
与底面 所成锐二面角的余弦值;
所成锐二面角的余弦值;
已知函数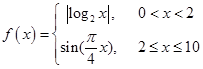 ,若存在实数
,若存在实数 满足
满足 ,且
,且 ,则
,则 的取值范围( )
的取值范围( )
| A.(20,32) | B.(9,21) | C.(8,24) | D.(15,25) |
以下四个命题中:
①为了了解800名学生对学校某项教改试验的意见,打算从中抽取一个容量为 的样本,考虑用系统抽样,则分段的间隔
的样本,考虑用系统抽样,则分段的间隔 为40.
为40.
②线性回归直线方程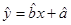 恒过样本中心
恒过样本中心 ,且至少过一个样本点;
,且至少过一个样本点;
③在某项测量中,测量结果ξ服从正态分布 .若ξ在
.若ξ在 内取值的概率为
内取值的概率为 ,则ξ在
,则ξ在 内取值的概率为
内取值的概率为 ;
;
其中真命题的个数为( )
A. |
B. |
C. |
D. |