初中数学垂径定理试题

如图， $\mathit{AB}$是 $\odot O$的直径， $\mathit{AC}$是上半圆的弦，过点 $C$作 $\odot O$的切线 $\mathit{DE}$交 $\mathit{AB}$的延长线于点 $E$，过点 $A$作切线 $\mathit{DE}$的垂线，垂足为 $D$，且与 $\odot O$交于点 $F$，设 $\angle \mathit{DAC}$， $\angle \mathit{CEA}$的度数分别是 $\alpha$， $\beta$．

（1）用含 $\alpha$的代数式表示 $\beta$，并直接写出 $\alpha$的取值范围；

（2）连接 $\mathit{OF}$与 $\mathit{AC}$交于点 $O\text{'}$，当点 $O\text{'}$是 $\mathit{AC}$的中点时，求 $\alpha$， $\beta$的值．

如图， $\mathit{AB}$是 $\odot O$的直径，弦 $\mathit{CD}\perp \mathit{AB}$于点 $E$， $\angle \mathit{CDB}=30°$， $\odot O$的半径为 $5\mathit{cm}$，则圆心 $O$到弦 $\mathit{CD}$的距离为 $($　　 $)$

A． $\frac{5}{2}\mathit{cm}$B． $3\mathit{cm}$C． $3\sqrt{3}\mathit{cm}$D． $6\mathit{cm}$

如图，已知 $\odot O$的半径为 $6\mathit{cm}$，弦 $\mathit{AB}$的长为 $8\mathit{cm}$， $P$是 $\mathit{AB}$延长线上一点， $\mathit{BP}=2\mathit{cm}$，则 $\tan \angle \mathit{OPA}$的值是　　．

如图， $\mathit{AB}$是 $\odot O$的直径，弦 $\mathit{CD}\perp \mathit{AB}$于点 $E$，若 $\mathit{AB}=8$， $\mathit{CD}=6$，则 $\mathit{BE}=$　　．

如图， $\mathit{AB}$是 $\odot O$的直径，弦 $\mathit{CD}\perp \mathit{AB}$于点 $E$，点 $F$是 $\odot O$上一点，且 $\stackrel{̂}{\mathit{AC}}=\stackrel{̂}{\mathit{CF}}$，连接 $\mathit{FB}$， $\mathit{FD}$， $\mathit{FD}$交 $\mathit{AB}$于点 $N$．

（1）若 $\mathit{AE}=1$， $\mathit{CD}=6$，求 $\odot O$的半径；

（2）求证： $\mathit{\Delta BNF}$为等腰三角形；

（3）连接 $\mathit{FC}$并延长，交 $\mathit{BA}$的延长线于点 $P$，过点 $D$作 $\odot O$的切线，交 $\mathit{BA}$的延长线于点 $M$．求证： $\mathit{ON}·\mathit{OP}=\mathit{OE}·\mathit{OM}$．

如图， $\mathit{BD}$是 $\odot O$的直径，弦 $\mathit{BC}$与 $\mathit{OA}$相交于点 $E$， $\mathit{AF}$与 $\odot O$相切于点 $A$，交 $\mathit{DB}$的延长线于点 $F$， $\angle F=30°$， $\angle \mathit{BAC}=120°$， $\mathit{BC}=8$．

（1）求 $\angle \mathit{ADB}$的度数；

（2）求 $\mathit{AC}$的长度．

如图， $\mathit{BM}$是以 $\mathit{AB}$为直径的 $\odot O$的切线， $B$为切点， $\mathit{BC}$平分 $\angle \mathit{ABM}$，弦 $\mathit{CD}$交 $\mathit{AB}$于点 $E$， $\mathit{DE}=\mathit{OE}$．

（1）求证： $\mathit{\Delta ACB}$是等腰直角三角形；

（2）求证： $O{A}^2=\mathit{OE}·\mathit{DC}$；

（3）求 $\tan \angle \mathit{ACD}$的值．

如图，在 $\odot O$中， $\mathit{AB}$是 $\odot O$的直径， $\mathit{AB}=10$， $\stackrel{̂}{\mathit{AC}}=\stackrel{̂}{\mathit{CD}}=\stackrel{̂}{\mathit{DB}}$，点 $E$是点 $D$关于 $\mathit{AB}$的对称点， $M$是 $\mathit{AB}$上的一动点，下列结论：① $\angle \mathit{BOE}=60°$；② $\angle \mathit{CED}=\frac{1}{2}\angle \mathit{DOB}$；③ $\mathit{DM}\perp \mathit{CE}$；④ $\mathit{CM}+\mathit{DM}$的最小值是10，上述结论中正确的个数是 $($　　 $)$

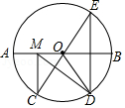
A．1B．2C．3D．4

如图， $\odot O$的直径 $\mathit{AB}$垂直于弦 $\mathit{CD}$， $\angle \mathit{CAB}=36°$，则 $\angle \mathit{BCD}$的大小是 $($　　 $)$

A． $18°$B． $36°$C． $54°$D． $72°$

如图， $\mathit{AB}$是 $\odot O$的直径，弦 $\mathit{CD}\perp \mathit{AB}$，垂足为 $H$，连接 $\mathit{AC}$，过 $\stackrel{̂}{\mathit{BD}}$上一点 $E$作 $\mathit{EG}//\mathit{AC}$交 $\mathit{CD}$的延长线于点 $G$，连接 $\mathit{AE}$交 $\mathit{CD}$于点 $F$，且 $\mathit{EG}=\mathit{FG}$，连接 $\mathit{CE}$．

（1）求证： $\mathit{\Delta ECF}\backsim \mathit{\Delta GCE}$；

（2）求证： $\mathit{EG}$是 $\odot O$的切线；

（3）延长 $\mathit{AB}$交 $\mathit{GE}$的延长线于点 $M$，若 $\tan G=\frac{3}{4}$， $\mathit{AH}=3\sqrt{3}$，求 $\mathit{EM}$的值．

通过对下面数学模型的研究学习，解决问题．

【模型呈现】

如图，在 $\text{Rt}\Delta \text{ABC}$， $\angle \mathit{ACB}=90°$，将斜边 $\mathit{AB}$绕点 $A$顺时针旋转 $90°$得到 $\mathit{AD}$，过点 $D$作 $\mathit{DE}\perp \mathit{AC}$于点 $E$，可以推理得到 $\mathit{\Delta ABC}\cong \mathit{\Delta DAE}$，进而得到 $\mathit{AC}=\mathit{DE}$， $\mathit{BC}=\mathit{AE}$．

我们把这个数学模型称为“ $K$型”．

推理过程如下：

【模型应用】

如图，在 $\text{Rt}\Delta \text{ABC}$内接于 $\odot O$， $\angle \mathit{ACB}=90°$， $\mathit{BC}=2$，将斜边 $\mathit{AB}$绕点 $A$顺时针旋转一定的角度得到 $\mathit{AD}$，过点 $D$作 $\mathit{DE}\perp \mathit{AC}$于点 $E$， $\angle \mathit{DAE}=\angle \mathit{ABC}$， $\mathit{DE}=1$，连接 $\mathit{DO}$交 $\odot O$于点 $F$．

（1）求证： $\mathit{AD}$是 $\odot O$的切线；

（2）连接 $\mathit{FC}$交 $\mathit{AB}$于点 $G$，连接 $\mathit{FB}$．求证： $F{G}^2=\mathit{GO}·\mathit{GB}$．

如图是由两个长方形组成的工件平面图（单位： $\mathit{mm})$，直线 $l$是它的对称轴，能完全覆盖这个平面图形的圆面的最小半径是　　 $\mathit{mm}$．

如图， $\mathit{AB}$为 $\odot O$直径， $C$为 $\odot O$上一点，点 $D$是 $\stackrel{̂}{\mathit{BC}}$的中点， $\mathit{DE}\perp \mathit{AC}$于 $E$， $\mathit{DF}\perp \mathit{AB}$于 $F$．

（1）判断 $\mathit{DE}$与 $\odot O$的位置关系，并证明你的结论；

（2）若 $\mathit{OF}=4$，求 $\mathit{AC}$的长度．

如图， $\mathit{AB}$是圆 $O$的直径，弦 $\mathit{CD}\perp \mathit{AB}$， $\angle \mathit{BCD}=30°$， $\mathit{CD}=4\sqrt{3}$，则 $S_{\mathit{阴影}}=($　　 $)$

A． $2\pi$B． $\frac{8}{3}\pi$C． $\frac{4}{3}\pi$D． $\frac{3}{8}\pi$

已知：△ ABC内接于⊙ O， D是 $\stackrel{̂}{\mathit{BC}}$ 上一点， $\mathit{OD}\perp \mathit{BC}$ ，垂足为 H．

（1）如图1，当圆心 O在 AB边上时，求证： $\mathit{AC}＝2\mathit{OH}$ ；

（2）如图2，当圆心 O在△ ABC外部时，连接 AD、 CD， AD与 BC交于点 P，求证： $\angle \mathit{ACD}＝\angle \mathit{APB}$ ；

（3）在（2）的条件下，如图3，连接 BD， E为⊙ O上一点，连接 DE交 BC于点 Q、交 AB于点 N，连接 OE， BF为⊙ O的弦， $\mathit{BF}\perp \mathit{OE}$ 于点 R交 DE于点 G，若 $\angle \mathit{ACD}﹣\angle \mathit{ABD}＝2\angle \mathit{BDN}$ ， $\mathit{AC}=5\sqrt{5}$ ， $\mathit{BN}=3\sqrt{5}$ , $\mathrm{}\tan \angle \mathit{ABC}=\frac{1}{2}$ ,求 BF的长．