如图,点 在直线 上,过点 作 交直线 于点 ,以 为边在△ 外侧作等边三角形 ,再过点 作 ,分别交直线 和 于 , 两点,以 为边在△ 外侧作等边三角形 , 按此规律进行下去,则第 个等边三角形 的面积为 .(用含 的代数式表示)

如图,以边长为 的正三角形纸板的各顶点为端点,在各边上分别截取 长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形.把它们沿图中虚线剪掉,用剩下的纸板折成一个底为正三角形的无盖柱形盒子,则它的容积为 .

如图, 是等边三角形, ,分别以 , , 为圆心,以2为半径作弧,则图中阴影部分的面积是 .

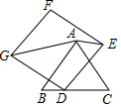
已知: 和 均为等边三角形,连接 , ,点 , , 分别为 , , 中点.
(1)当 绕点 旋转时,如图1,则 的形状为 ,说明理由;
(2)在 旋转的过程中,当 , , 三点共线时,如图2,若 , ,求线段 的长;
(3)在 旋转的过程中,若 , ,则 的周长是否存在最大值和最小值,若存在,直接写出最大值和最小值;若不存在,说明理由.

如图,等边△ 的周长为1,作 于 ,在 的延长线上取点 ,使 ,连接 ,以 为边作等边△ ;作 于 ,在 的延长线上取点 ,使 ,连接 ,以 为边作等边△ ; 且点 , , , 都在直线 同侧,如此下去,则△ ,△ ,△ , ,△ 的周长和为 . ,且 为整数)

已知:
和
按如图所示方式放置,点
在
内,连接
、
和
,且
.
(1)如图①,当 和 均为等边三角形时,试确定 、 、 三条线段的关系,并说明理由;
(2)如图②,当 , 时,试确定 、 、 三条线段的关系,并说明理由;
(3)如图③,当 时,请直接写出 、 、 三条线段的关系.
如图, 是等边三角形,点 为 边上一点, ,以点 为顶点作正方形 ,且 ,连接 , .若将正方形 绕点 旋转一周,当 取最小值时, 的长为 .
在边长为2的等边三角形 中, 是 边上任意一点,过点 分别作 , , 、 分别为垂足.
(1)求证:不论点 在 边的何处时都有 的长恰好等于三角形 一边上的高;
(2)当 的长为何值时,四边形 的面积最大,并求出最大值.

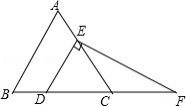
在等边 中,点 , 分别在边 、 上,若 ,过点 作 ,过点 作 ,交 的延长线于点 ,求 的长.
如图,等边三角形 中, ,垂足为 ,点 在线段 上, ,则 等于

| A. |
|
B. |
|
C. |
|
D. |
|
如图,等边三角形 中, ,垂足为 ,点 在线段 上, ,则 等于

| A. |
|
B. |
|
C. |
|
D. |
|
二次函数 的图象如图所示,若线段 在 轴上,且 为 个单位长度,以 为边作等边 ,使点 落在该函数 轴右侧的图象上,则点 的坐标为 .
