如图,在菱形 中, , ,点 是这个菱形内部或边上的一点.若以 , , 为顶点的三角形是等腰三角形,则 , , 两点不重合)两点间的最短距离为 .

如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点 是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段 绕三角形顶点顺时针转过的角度是

A. B. C. D.
如图所示,正方形 的边长为6, 是等边三角形,点 在正方形 内,在对角线 上有一点 ,使 的和最小,则这个最小值为 .

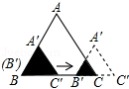
如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为 ,两个三角形重叠面积为 ,则 关于 的函数图象是
A.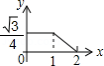 B.
B.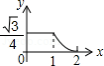
C. D.
D.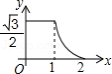
小颖同学在手工制作中,把一个边长为 的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为
A. B. C. D.
已知线段 直线 于点 ,点 在直线 上,分别以 、 为边作等边三角形 和等边三角形 ,直线 交直线 于点 .
(1)当点 在线段 上时,如图①,求证: ;
(2)当点 在线段 的延长线上时,如图②;当点 在线段 的延长线上时,如图③,请分别写出线段 、 、 之间的数量关系,在图②、图③中选一个进行证明;
(3)在(1)、(2)的条件下,若 , ,则 .

如图, 为等边三角形,点 从 出发,沿 作匀速运动,则线段 的长度 与运动时间 之间的函数关系大致是

A. B.
B.
C. D.
D.
已知等边 的边长为12, 是 上的动点,过 作 于点 ,过 作 于点 ,过 作 于点 .当 与 重合时, 的长是
A.3B.4C.8D.9
如图,边长为4的等边 中, 、 分别为 , 的中点,则 的面积是
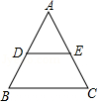
A. B. C. D.
已知等边三角形的边长为3,点 为等边三角形内任意一点,则点 到三边的距离之和为
A. B. C. D.不能确定
如图,点 是边长为 的等边 的内心,将 绕点 逆时针旋转 得到△ , 交 于点 , 交 于点 ,则 .
