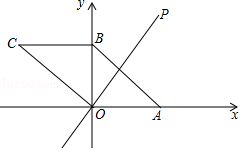
如图,在直角坐标系 中,矩形 的顶点 、 分别在 轴和 轴正半轴上,点 的坐标是 ,点 是 边上一动点(不与点 、点 重合),连接 、 ,过点 作射线 交 的延长线于点 ,交 边于点 ,且 ,令 , .
(1)当 为何值时, ?
(2)求 与 的函数关系式,并写出 的取值范围;
(3)在点 的运动过程中,是否存在 ,使 的面积与 的面积之和等于 的面积?若存在,请求 的值;若不存在,请说明理由.

如图,点 , , , 均在坐标轴上,且 , ,若点 , 的坐标分别为 , ,则点 的坐标为 .

如图,在平面直角坐标系中,每个最小方格的边长均为1个单位长,P1,P2,P3,…,均在格点上,其顺序按图中“→”方向排列,如: , , , , , …根据这个规律,点P2016的坐标为 .

平面直角坐标系中有两点M(a,b),N(c,d),规定(a,b)⊕(c,d)=(a+c,b+d),则称点Q(a+c,b+d)为M,N的“和点”.若以坐标原点O与任意两点及它们的“和点”为顶点能构成四边形,则称这个四边形为“和点四边形”,现有点A(2,5),B(﹣1,3),若以O,A,B,C四点为顶点的四边形是“和点四边形”,则点C的坐标是 .
如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上. 且 ,OB,OC的长分别是一元二次方程 的两个根 .
(1)求点A和点B的坐标.
(2)点P是线段OB上的一个动点(点P不与点O,B重合),过点P的直线l与y轴平行,直线l交边OA或边AB于点Q,交边OC或边BC于点R.设点P的横坐标为t,线段QR的长度为m.已知 时,直线l恰好过点C.当 时,求m关于t的函数关系式.
(3)当 时,请直接写出点P的坐标.

如图,等边三角形的顶点A(1,1)、B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次変换,如果这样连续经过2016次变换后,等边△ABC的顶点C的坐标为 .

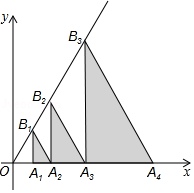
如图, 、 、 、… 都是等边三角形,其中 、 、… 都与x轴垂直,点A1、A2、…An都在x轴上,点B1、B2、…Bn都在直线 上,已知 ,则点A2016的坐标为 .
如图,在平面直角坐标系中, , , .先将四边形ABCD沿x轴翻折,再向右平移8个单位长度,向下平移1个单位长度后,得到四边形A1B1C1D1,最后将四边形A1B1C1D1,绕着点A1旋转,使旋转后的四边形对角线的交点落在x轴上,则旋转后的四边形对角线的交点坐标为( )

A.(4,0)B.(5,0)
C.(4,0)或(﹣4,0)D.(5,0)或(﹣5,0)
如图,在平面直角坐标系中,矩形 AOCB的两边 OA、 OC分别在 x轴和 y轴上,且 OA=2, OC=1.在第二象限内,将矩形 AOCB以原点 O为位似中心放大为原来的 倍,得到矩形 A 1 OC 1 B 1,再将矩形 A 1 OC 1 B 1以原点 O为位似中心放大 倍,得到矩形 A 2 OC 2 B 2…,以此类推,得到的矩形 A n O∁ n B n的对角线交点的坐标为 .

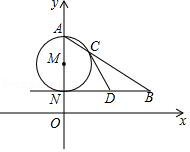
如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.
如图,在平面直角坐标系xOy中,▱ABCO的顶点A,B的坐标分别是A(3,0),B(0,2).动点P在直线 上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与▱ABCO的边相切时,P点的坐标为 .