高中数学数列综合试题

设数列{a_n}的前n项和S_n=n²，则a₈的值为（）

A．15

B．16

C．49

D．64

已知等比数列{a_n}的前n项和为S_n，若S₄、S₂、S₃成等差数列，且a₂+a₃+a₄=﹣18，若S_n≥2016，则n的取值范围为 ．

已知{a_n}是正项数列，a₁=1，且点（，a_n+1）（n∈N^*）在函数y=x²+1的图象上．
（1）求数列{a_n}的通项公式；
（2）若列数{b_n}满足b₁=1，b_n+1=b_n+2，求证：b_nb_n+2＜b．

数列{a_n}的通项a_n=n²（cos²﹣sin²），其前n项和为S_n，则S₃₀为 ．

已知{a_n}为等差数列，若a₁+a₅+a₉=π，则cos（a₂+a₈）的值为（）

A．

B．

C．

D．

在正项数列{a_n}中，a₁=1，点A_n（）在曲线y²﹣x²=1上，数列{b_n}中，点（b_n，T_n）在直线y=﹣x+1上，其中T_n是数列{b_n}的前n项和．
（1）求数列{a_n}，{b_n}的通项公式a_n，b_n；
（2）若c_n=a_n•b_n，数列{c_n}的前n项和S_n．

已知等差数列{a_n}的前n项和S_n满足S₃=0，S₅=﹣5，
（1）求{a_n}的通项公式；
（2）求数列{}的前n项和．

等差数列{a_n}的前m项和为30，前2m项和为100，则它的前3m项和为 ．

设数列{a_n}满足：a₁=2，a_n+1=1﹣，记数列{a_n}的前n项之积为T_n，则T₂₀₁₆的值为（）

A．﹣

B．﹣1

C．

D．1

设数列{a_n}的前n项和为Sn，且S_n=4a_n﹣p，其中p是不为零的常数．
（1）证明：数列{a_n}是等比数列；
（2）当p=3时，若数列{b_n}满足b_n+1=b_n+a_n（n∈N^*），b₁=2，求数列{b_n}的通项公式．

已知等比数列{a_n}的各项均为正数，且2a₁，成等差数列，a₂，，a₆成等比数列．
（1）求数列{a_n}的通项公式；
（2）设b_n=log₃，记S_n=，求S_n．

设p：“lgx，lg（x+1），lg（x+3）成等差数列”，q：“2^x+1﹣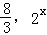，3成等比数列”，则p是q的（）

A．充分不必要条件	B．必要不充分条件
C．充要条件	D．既不充分又不必要条件

等差数列{a_n}的前n项和为S_n，若a₂+a₇+a₁₂=15，则S₁₃的值是（）

A．45

B．65

C．80

D．130

在数列{a_n}中，已知．
（1）求数列{a_n}的通项公式；
（2）求证：数列{b_n}是等差数列；
（3）设数列{c_n}满足c_n=a_n+b_n，求{c_n}的前n项和S_n．

若{a_n}为等差数列，S_n是其前n项和，且，则tana₆的值为（）

A．

B．

C．

D．