2022年中考数学专题:二次函数(二)
已知二次函数 的图象经过第一象限的点 ,则一次函数 的图象不经过
| A. |
第一象限 |
B. |
第二象限 |
C. |
第三象限 |
D. |
第四象限 |
如图,已知抛物线 的对称轴在 轴右侧,抛物线与 轴交于点 和点 ,与 轴的负半轴交于点 ,且 ,则下列结论:① ;② ;③ ;④当 时,在 轴下方的抛物线上一定存在关于对称轴对称的两点 , (点 在点 左边),使得 ,其中正确的有

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
已知 、 两点的坐标分别为 、 ,线段 上有一动点 ,过点 作 轴的平行线交抛物线 于 , 、 , 两点.若 ,则 的取值范围为
| A. |
|
B. |
|
C. |
|
D. |
|
定义: , , 为二次函数 的特征数,下面给出特征数为 , , 的二次函数的一些结论:①当 时,函数图象的对称轴是 轴;②当 时,函数图象过原点;③当 时,函数有最小值;④如果 ,当 时, 随 的增大而减小.其中所有正确结论的序号是 .
将二次函数 的图象在 轴上方的部分沿 轴翻折后,所得新函数的图象如图所示.当直线 与新函数的图象恰有3个公共点时, 的值为

| A. |
或 |
B. |
或 |
C. |
或 |
D. |
或 |
已知二次函数 的图象经过第一象限的点 ,则一次函数 的图象不经过
A.第一象限B.第二象限C.第三象限D.第四象限
下表中列出的是一个二次函数的自变量 与函数 的几组对应值:
|
|
|
0 |
1 |
3 |
|
|
|
6 |
|
|
|
|
下列各选项中,正确的是
| A. |
这个函数的图象开口向下 |
| B. |
这个函数的图象与 轴无交点 |
| C. |
这个函数的最小值小于 |
| D. |
当 时, 的值随 值的增大而增大 |
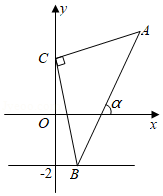
如图,已知点 ,点 为直线 上的一动点,点 , , 于点 ,连接 .若直线 与 正半轴所夹的锐角为 ,那么当 的值最大时, 的值为 .
关于抛物线 ,给出下列结论:
①当 时,抛物线与直线 没有交点;
②若抛物线与 轴有两个交点,则其中一定有一个交点在点 与 之间;
③若抛物线的顶点在点 , , 围成的三角形区域内(包括边界),则 .
其中正确结论的序号是 .
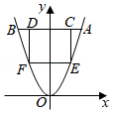
如图,在平面直角坐标系中,点 在抛物线 上,过点 作 轴的垂线,交抛物线于另一点 ,点 、 在线段 上,分别过点 、 作 轴的垂线交抛物线于 、 两点.当四边形 为正方形时,线段 的长为 .
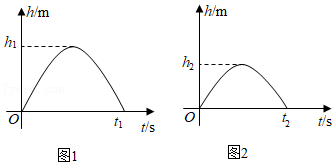
以初速度 (单位: 从地面竖直向上抛出小球,从抛出到落地的过程中,小球的高度 (单位: 与小球的运动时间 (单位: 之间的关系式是 .现将某弹性小球从地面竖直向上抛出,初速度为 ,经过时间 落回地面,运动过程中小球的最大高度为 (如图 ;小球落地后,竖直向上弹起,初速度为 ,经过时间 落回地面,运动过程中小球的最大高度为 (如图 .若 ,则 .
从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度 (单位: 与它距离喷头的水平距离 (单位: 之间满足函数关系式 喷出水珠的最大高度是 .

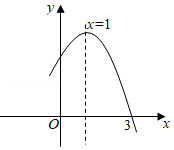
如图是抛物线 的部分图象,图象过点 ,对称轴为直线 ,有下列四个结论:① ;② ;③ 的最大值为3;④方程 有实数根.其中正确的为 (将所有正确结论的序号都填入).
已知抛物线 与 轴交于 , 两点(点 在点 的左侧)与 轴交于点 ,点 在抛物线上, 是该抛物线对称轴上一动点,当 的值最小时, 的面积为 .
如图,在平面直角坐标系中, 为坐标原点,点 为 轴正半轴上的一个动点,过点 的直线与二次函数 的图象交于 、 两点,且 , 为 的中点,设点 的坐标为 , ,写出 关于 的函数表达式为: .

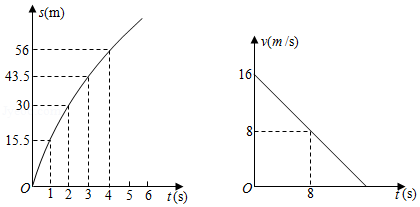
公路上正在行驶的甲车,发现前方 处沿同一方向行驶的乙车后,开始减速,减速后甲车行驶的路程 (单位: 、速度 (单位: 与时间 (单位: 的关系分别可以用二次函数和一次函数表示,其图象如图所示.
(1)当甲车减速至 时,它行驶的路程是多少?
(2)若乙车以 的速度匀速行驶,两车何时相距最近,最近距离是多少?
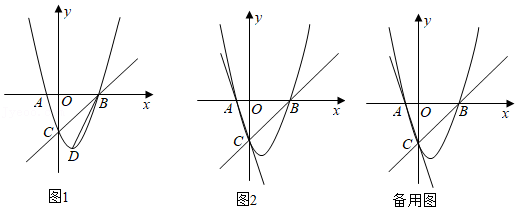
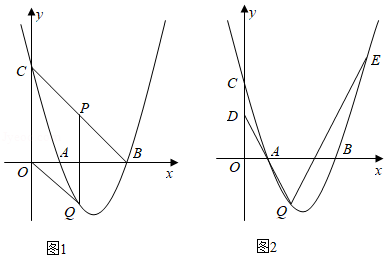
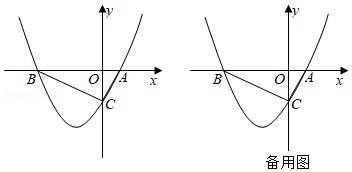
在平面直角坐标系中,抛物线 与 轴交于点 和点 ,与 轴交于点 ,顶点 的坐标为 .
(1)直接写出抛物线的解析式;
(2)如图1,若点 在抛物线上且满足 ,求点 的坐标;
(3)如图2, 是直线 上一个动点,过点 作 轴交抛物线于点 , 是直线 上一个动点,当 为等腰直角三角形时,直接写出此时点 及其对应点 的坐标.
如图,在平面直角坐标系中,已知抛物线 交 轴于 、 两点,交 轴于点 .
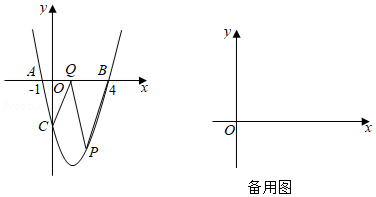
(1)求该抛物线的表达式;
(2)点 为第四象限内抛物线上一点,连接 ,过点 作 交 轴于点 ,连接 ,求 面积的最大值及此时点 的坐标;
(3)在(2)的条件下,将抛物线 向右平移经过点 , 时,得到新抛物线 ,点 在新抛物线的对称轴上,在坐标平面内是否存在一点 ,使得以 、 、 、 为顶点的四边形为矩形,若存在,请写出点 的坐标;若不存在,请说明理由.
参考:若点 , 、 , ,则线段 的中点 的坐标为 , .
在平面直角坐标系中,抛物线 与 轴交于点 和点 , ,顶点坐标记为 , .抛物线 的顶点坐标记为 , .
(1)写出 点坐标;
(2)求 , 的值(用含 的代数式表示)
(3)当 时,探究 与 的大小关系;
(4)经过点 和点 的直线与抛物线 , 的公共点恰好为3个不同点时,求 的值.
如图,已知抛物线 与 轴交于点 和 ,与 轴交于点 ,对称轴为直线 .
(1)求抛物线的解析式;
(2)如图1,若点 是线段 上的一个动点(不与点 , 重合),过点 作 轴的平行线交抛物线于点 ,连接 ,当线段 长度最大时,判断四边形 的形状并说明理由;
(3)如图2,在(2)的条件下, 是 的中点,过点 的直线与抛物线交于点 ,且 .在 轴上是否存在点 ,得 为等腰三角形?若存在,求点 的坐标;若不存在,请说明理由.
如图,在平面直角坐标系中, 的边 在 轴上, ,且线段 的长是方程 的根,过点 作 轴,垂足为 , ,动点 以每秒1个单位长度的速度,从点 出发,沿线段 向点 运动,到达点 停止.过点 作 轴的垂线,垂足为 ,以 为边作正方形 ,点 在线段 上,设正方形 与 重叠部分的面积为 ,点 的运动时间为 秒.
(1)求点 的坐标;
(2)求 关于 的函数关系式,并写出自变量 的取值范围;
(3)当点 落在线段 上时,坐标平面内是否存在一点 ,使以 、 、 、 为顶点的四边形是平行四边形?若存在,直接写出点 的坐标;若不存在,请说明理由.

二次函数 的图象交 轴于原点 及点 .
感知特例
(1)当 时,如图1,抛物线 上的点 , , , , 分别关于点 中心对称的点为 , , , , ,如表:
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
①补全表格;
②在图1中描出表中对称后的点,再用平滑的曲线依次连接各点,得到的图象记为 .

形成概念
我们发现形如(1)中的图象 上的点和抛物线 上的点关于点 中心对称,则称 是 的“孔像抛物线”.例如,当 时,图2中的抛物线 是抛物线 的“孔像抛物线”.

探究问题
(2)①当 时,若抛物线 与它的“孔像抛物线” 的函数值都随着 的增大而减小,则 的取值范围为 ;
②在同一平面直角坐标系中,当 取不同值时,通过画图发现存在一条抛物线与二次函数 的所有“孔像抛物线” 都有唯一交点,这条抛物线的解析式可能是 (填“ ”或“ ”或“ ”或“ ”,其中 ;
③若二次函数 及它的“孔像抛物线”与直线 有且只有三个交点,求 的值.
如图,在平面直角坐标系中,抛物线 经过坐标原点,与 轴正半轴交于点 ,点 是抛物线上一动点.
(1)如图1,当 , ,且 时,
①求点 的坐标;
②若点 , 在该抛物线上,连接 , , 是线段 上一动点(点 与点 , 不重合),过点 作 ,交 轴于点 ,线段 与 是否相等?请说明理由;
(2)如图2,该抛物线的对称轴交 轴于点 ,点 在对称轴上,当 , ,且直线 交 轴的负半轴于点 时,过点 作 轴的垂线,交直线 于点 , 为 轴上一点,点 的坐标为 ,连接 .若 ,求证:射线 平分 .
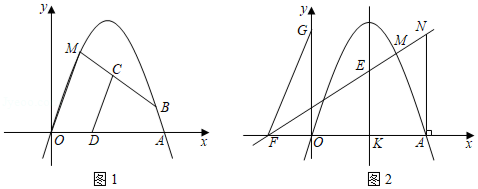








 粤公网安备 44130202000953号
粤公网安备 44130202000953号