二次函数 的图象交 轴于原点 及点 .
感知特例
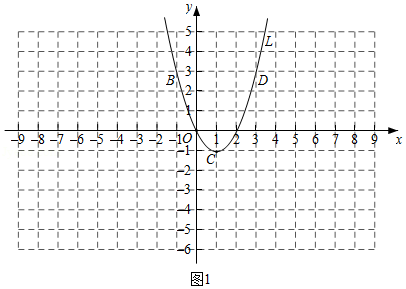
(1)当 时,如图1,抛物线 上的点 , , , , 分别关于点 中心对称的点为 , , , , ,如表:
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
①补全表格;
②在图1中描出表中对称后的点,再用平滑的曲线依次连接各点,得到的图象记为 .
形成概念
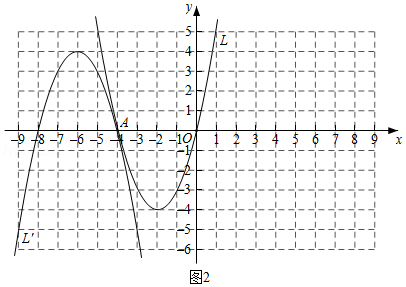
我们发现形如(1)中的图象 上的点和抛物线 上的点关于点 中心对称,则称 是 的“孔像抛物线”.例如,当 时,图2中的抛物线 是抛物线 的“孔像抛物线”.
探究问题
(2)①当 时,若抛物线 与它的“孔像抛物线” 的函数值都随着 的增大而减小,则 的取值范围为 ;
②在同一平面直角坐标系中,当 取不同值时,通过画图发现存在一条抛物线与二次函数 的所有“孔像抛物线” 都有唯一交点,这条抛物线的解析式可能是 (填“ ”或“ ”或“ ”或“ ”,其中 ;
③若二次函数 及它的“孔像抛物线”与直线 有且只有三个交点,求 的值.
相关知识点
推荐套卷

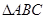 中,
中, 是
是 与
与 的平分线
的平分线 和
和 的交点,通过分析发现
的交点,通过分析发现 ,理由如下:
,理由如下:
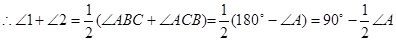

 的平分线
的平分线 与
与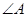 有怎样的关系?请说明理由.
有怎样的关系?请说明理由.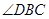 与外角
与外角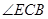 的平分线
的平分线

 件(
件( 粤公网安备 44130202000953号
粤公网安备 44130202000953号