2017年全国统一高考数学试卷(上海卷)
设双曲线 ﹣ =1(b>0)的焦点为F 1、F 2, P为该双曲线上的一点,若|PF 1|=5,则|PF 2|=________.
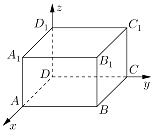
如图,以长方体ABCD﹣A 1B 1C 1D 1的顶点D为坐标原点,过D的三条棱所在的直线为坐标轴,建立空间直角坐标系,若 的坐标为(4,3,2),则 的坐标是________.
定义在(0,+∞)上的函数y=f(x)的反函数为y=f ﹣ 1(x),若g(x)= 为奇函数,则f ﹣ 1(x)=2的解为________.
已知四个函数:①y=﹣x,②y=- ,③y=x 3 , ④ ,从中任选2个,则事件"所选2个函数的图象有且仅有一个公共点"的概率为________.
已知数列{a n}和{b n},其中a n=n 2,n∈N *, {b n}的项是互不相等的正整数,若对于任意n∈N *, {b n}的第a n项等于{a n}的第b n项,则 =________.
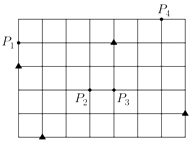
如图,用35个单位正方形拼成一个矩形,点P 1、P 2、P 3、P 4以及四个标记为"▲"的点在正方形的顶点处,设集合Ω={P 1 , P 2 , P 3 , P 4},点P∈Ω,过P作直线l P , 使得不在l P上的"▲"的点分布在l P的两侧.用D 1(l P)和D 2(l P)分别表示l P一侧和另一侧的"▲"的点到l P的距离之和.若过P的直线l P中有且只有一条满足D 1(l P)=D 2(l P),则Ω中所有这样的P为________.
在数列{a n}中,a n=(﹣ ) n , n∈N * , 则 a n( )
| A. |
等于 |
B. |
等于0 |
C. |
等于 |
D. |
不存在 |
已知a、b、c为实常数,数列{x n}的通项x n=an 2+bn+c,n∈N *,则"存在k∈N *,使得x 100+k、x 200+k、x 300+k成等差数列"的一个必要条件是( )
| A. |
a≥0 |
B. |
b≤0 |
C. |
c=0 |
D. |
a﹣2b+c=0 |
在平面直角坐标系xOy中,已知椭圆C 1: =1和C 2:x 2+ =1.P为C 1上的动点,Q为C 2上的动点,w是 的最大值.记Ω={(P,Q)|P在C 1上,Q在C 2上,且 =w},则Ω中元素个数为( )
| A. |
2个 |
B. |
4个 |
C. |
8个 |
D. |
无穷个 |
如图,直三棱柱ABC﹣A 1B 1C 1的底面为直角三角形,两直角边AB和AC的长分别为4和2,侧棱AA 1的长为5.
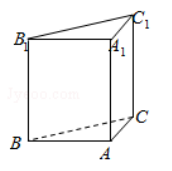
(1)求三棱柱ABC﹣A 1B 1C 1的体积;
(2)设M是BC中点,求直线A 1M与平面ABC所成角的大小.
已知函数f(x)=cos 2x﹣sin 2x+ ,x∈(0,π).
(1)求f(x)的单调递增区间;
(2)设△ABC为锐角三角形,角A所对边a= ,角B所对边b=5,若f(A)=0,求△ABC的面积.
根据预测,某地第n(n∈N *)个月共享单车的投放量和损失量分别为a n和b n(单位:辆),其中a n= ,b n=n+5,第n个月底的共享单车的保有量是前n个月的累计投放量与累计损失量的差.
(1)求该地区第4个月底的共享单车的保有量;
(2)已知该地共享单车停放点第n个月底的单车容纳量S n=﹣4(n﹣46) 2+8800(单位:辆).设在某月底,共享单车保有量达到最大,问该保有量是否超出了此时停放点的单车容纳量?
在平面直角坐标系xOy中,已知椭圆Γ: =1,A为Γ的上顶点,P为Γ上异于上、下顶点的动点,M为x正半轴上的动点.
(1)若P在第一象限,且|OP|= ,求P的坐标;
(2)设P( ),若以A、P、M为顶点的三角形是直角三角形,求M的横坐标;
(3)若|MA|=|MP|,直线AQ与Γ交于另一点C,且 , ,求直线AQ的方程.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号