2018年黑龙江省绥化市中考数学试卷

$-\frac{3}{2}$的相反数是 $($　　 $)$

A．1.5B． $\frac{2}{3}$C． $-1.5$D． $-\frac{2}{3}$

下列图形中，既是中心对称图形又是轴对称图形的有 $($　　 $)$

A．4个B．3个C．2个D．1个

已知某物体的三视图如图所示，那么与它对应的物体是 $($　　 $)$

A．B．C．D．

下列运算正确的是 $($　　 $)$

A． $2a+3a=5a^2$B． $\sqrt{{(-5)}^2}=-5$

C． $a^3·a^4=a^{12}$D． ${(\pi -3)}^0=1$

若 $y=\frac{\sqrt{1-2x}}{x}$有意义，则 $x$的取值范围是 $($　　 $)$

A． $x⩽\frac{1}{2}$且 $x\ne 0$B． $x\ne \frac{1}{2}$C． $x⩽\frac{1}{2}$D． $x\ne 0$

已知反比例函数 $y=\frac{3}{x}$，下列结论中不正确的是 $($　　 $)$

A．其图象经过点 $(3,1)$

B．其图象分别位于第一、第三象限

C．当 $x>0$时， $y$随 $x$的增大而减小

D．当 $x>1$时， $y>3$

下列选项中，不能判定四边形 $\mathit{ABCD}$是平行四边形的是 $($　　 $)$

A． $\mathit{AD}//\mathit{BC}$， $\mathit{AB}//\mathit{CD}$B． $\mathit{AB}//\mathit{CD}$， $\mathit{AB}=\mathit{CD}$C． $\mathit{AD}//\mathit{BC}$， $\mathit{AB}=\mathit{DC}$D． $\mathit{AB}=\mathit{DC}$， $\mathit{AD}=\mathit{BC}$

某工厂新引进一批电子产品，甲工人比乙工人每小时多搬运30件电子产品，已知甲工人搬运300件电子产品所用的时间与乙工人搬运200件电子产品所用的时间相同．若设乙工人每小时搬运 $x$件电子产品，可列方程为 $($　　 $)$

A． $\frac{300}{x}=\frac{200}{x+30}$B． $\frac{300}{x-30}=\frac{200}{x}$C． $\frac{300}{x+30}=\frac{200}{x}$D． $\frac{300}{x}=\frac{200}{x-30}$

两个相似三角形的最短边分别为 $5\mathit{cm}$和 $3\mathit{cm}$，他们的周长之差为 $12\mathit{cm}$，那么大三角形的周长为 $($　　 $)$

A．14 $\mathit{cm}$B．16 $\mathit{cm}$C．18 $\mathit{cm}$D．30 $\mathit{cm}$

抛物线 $y=a{x}^2+\mathit{bx}+c(a\ne 0)$的部分图象如图所示，与 $x$轴的一个交点坐标为 $(4,0)$，抛物线的对称轴是 $x=1$．下列结论中：

① $\mathit{abc}>0$；

② $2a+b=0$；

③方程 $a{x}^2+\mathit{bx}+c=3$有两个不相等的实数根；

④抛物线与 $x$轴的另一个交点坐标为 $(-2,0)$；

⑤若点 $A(m,n)$在该抛物线上，则 $a{m}^2+\mathit{bm}+c⩽a+b+c$．

其中正确的有 $($　　 $)$

A．5个B．4个C．3个D．2个

某种病菌的形状为球形，直径约是 $0.000000102m$，用科学记数法表示这个数为　　．

在 $\frac{16}{3}$， $\sqrt{3}$， $\pi$， $-1.6$， $\sqrt{25}$这五个数中，有理数有　　个．

因式分解： $3a{x}^2-12a{y}^2=$　　．

三角形三边长分别为3， $2a-1$，4．则 $a$的取值范围是　　．

当 $x=2$时，代数式 $(\frac{2x+1}{x}+x)÷\frac{x+1}{x}$的值是　　．

如图， $\mathit{\Delta ABC}$是半径为2的圆内接正三角形，则图中阴影部分的面积是　　（结果用含 $\pi$的式子表示）．

如图，一块飞镖游戏板由大小相等的小正方形格子构成，向游戏板随机投掷一枚飞镖，击中黑色区域的概率是　　．

已知等腰三角形的一个外角为 $130°$，则它的顶角的度数为　　．

为了开展“阳光体育”活动，某班计划购买甲、乙两种体育用品（每种体育用品都购买），其中甲种体育用品每件20元，乙种体育用品每件30元，共用去150元，请你设计一下，共有　　种购买方案．

如图，一下水管道横截面为圆形，直径为 $100\mathit{cm}$，下雨前水面宽为 $60\mathit{cm}$，一场大雨过后，水面宽为 $80\mathit{cm}$，则水位上升　　 $\mathit{cm}$．

将一些圆按照如图方式摆放，从上向下有无数行，其中第一行有2个圆，第二行有4个圆，第三行有6个圆 $\dots$按此规律排列下去，则前50行共有圆　　个．

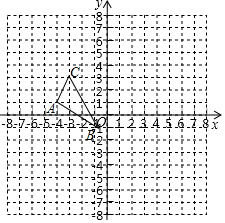
如图，在平面直角坐标系中， $\mathit{\Delta ABC}$的三个顶点的坐标分别为 $A(-4,1)$， $B(-1,-1)$， $C(-3,3)$．（每个小方格都是边长为1个单位长度的正方形）

（1）将 $\mathit{\Delta ABC}$先向上平移2个单位长度，再向右平移4个单位长度得到△ $A_1{B}_1{C}_1$（点 $A$、 $B$、 $C$的对应点分别为点 $A_1$、 $B_1$、 $C_1)$，画出平移后的△ $A_1{B}_1{C}_1$；

（2）将△ $A_1{B}_1{C}_1$绕着坐标原点 $O$顺时针旋转 $90°$得到△ $A_2{B}_2{C}_2$（点 $A_1$、 $B_1$、 $C_1$的对应点分别为点 $A_2$、 $B_2$、 $C_2)$，画出旋转后的△ $A_2{B}_2{C}_2$；

（3）求△ $A_1{B}_1{C}_1$在旋转过程中，点 $C_1$旋转到点 $C_2$所经过的路径的长．（结果用含 $\pi$的式子表示）

某校举办“打造平安校园”活动，随机抽取了部分学生进行校园安全知识测试．将这些学生的测试结果分为四个等级： $A$级：优秀； $B$级：良好； $C$级：及格； $D$级：不及格，并将测试结果绘制成如下统计图．请你根据图中信息，解答下列问题：

（1）本次参加校园安全知识测试的学生有多少人？

（2）计算 $B$级所在扇形圆心角的度数，并补全折线统计图；

（3）若该校有学生1000名，请根据测试结果，估计该校达到及格和及格以上的学生共有多少人？

如图，在 $\text{Rt}\Delta \text{ABC}$中， $\angle C=90°$， $\mathit{AC}=3$， $\mathit{BC}=4$， $D$、 $E$分别是斜边 $\mathit{AB}$、直角边 $\mathit{BC}$上的点，把 $\mathit{\Delta ABC}$沿着直线 $\mathit{DE}$折叠．

（1）如图1，当折叠后点 $B$和点 $A$重合时，用直尺和圆规作出直线 $\mathit{DE}$；（不写作法和证明，保留作图痕迹）

（2）如图2，当折叠后点 $B$落在 $\mathit{AC}$边上点 $P$处，且四边形 $\mathit{PEBD}$是菱形时，求折痕 $\mathit{DE}$的长．

已知关于 $x$的一元二次方程 $x^2-5x+2m=0$有实数根．

（1）求 $m$的取值范围；

（2）当 $m=\frac{5}{2}$时，方程的两根分别是矩形的长和宽，求该矩形外接圆的直径．

如图， $\mathit{AB}$是 $\odot O$的直径， $\mathit{AC}$为弦， $\angle \mathit{BA}$的平分线交 $\odot O$于点 $D$，过点 $D$的切线交 $\mathit{AC}$的延长线于点 $E$．

求证：（1） $\mathit{DE}\perp \mathit{AE}$；

（2） $\mathit{AE}+\mathit{CE}=\mathit{AB}$．

端午节期间，甲、乙两人沿同一路线行驶，各自开车同时去离家560千米的景区游玩，甲先以每小时60千米的速度匀速行驶1小时，再以每小时 $m$千米的速度匀速行驶，途中休息了一段时间后，仍按照每小时 $m$千米的速度匀速行驶，两人同时到达目的地，图中折线、线段分别表示甲、乙两人所走的路程 $y_{甲}\left(\mathit{km}\right)$， $y_{乙}\left(\mathit{km}\right)$与时间 $x\left(h\right)$之间的函数关系的图象．请根据图象提供的信息，解决下列问题：

（1）图中 $E$点的坐标是　   ，题中 $m=$　　 $\mathit{km}/h$，甲在途中休息　　 $h$；

（2）求线段 $\mathit{CD}$的解析式，并写出自变量 $x$的取值范围；

（3）两人第二次相遇后，又经过多长时间两人相距 $20\mathit{km}$？

如图，在矩形 $\mathit{ABCD}$中， $\mathit{AD}=5$， $\mathit{CD}=4$，点 $E$是 $\mathit{BC}$边上的点， $\mathit{BE}=3$，连接 $\mathit{AE}$， $\mathit{DF}\perp \mathit{AE}$交于点 $F$．

（1）求证： $\mathit{\Delta ABE}\cong \mathit{\Delta DFA}$；

（2）连接 $\mathit{CF}$，求 $\sin \angle \mathit{DCF}$的值；

（3）连接 $\mathit{AC}$交 $\mathit{DF}$于点 $G$，求 $\frac{\mathit{AG}}{\mathit{GC}}$的值．

已知直线 $y=\frac{1}{2}x+2$分别交 $x$轴、 $y$轴于 $A$、 $B$两点，抛物线 $y=\frac{1}{2}{x}^2+\mathit{mx}-2$经过点 $A$，和 $x$轴的另一个交点为 $C$．

（1）求抛物线的解析式；

（2）如图1，点 $D$是抛物线上的动点，且在第三象限，求 $\mathit{\Delta ABD}$面积的最大值；

（3）如图2，经过点 $M(-4,1)$的直线交抛物线于点 $P$、 $Q$，连接 $\mathit{CP}$、 $\mathit{CQ}$分别交 $y$轴于点 $E$、 $F$，求 $\mathit{OE}·\mathit{OF}$的值．

备注：抛物线顶点坐标公式 $(-\frac{b}{2a}$， $\frac{4\mathit{ac}-b^2}{4a})$