2015年全国统一高考文科数学试卷(上海卷)
在报名的3名男教师和6名女教师中,选取5人参加义务献血,要求男、女教师都有,则不同的选取方式的种数为(结果用数值表示).
来源:2015年全国普通高等学校招生统一考试文科数学
已知双曲线 的顶点重合, 的方程为 ,若 的一条渐近线的斜率是 的一条渐近线的斜率的2倍,则 的方程为.
来源:2015年全国普通高等学校招生统一考试文科数学
设 、 ,则" 、 均为实数"是" 是实数"的().
| A. | 充分非必要条件 |
| B. | 必要非充分条件 |
| C. | 充要条件 |
| D. | 既非充分又非必要条件 |
来源:2015年全国普通高等学校招生统一考试文科数学
如图,圆锥的顶点为
,底面的一条直径为
,
为半圆弧
的中点,
为劣弧
的中点.已知
,求三棱锥
的体积,并求异面直线
与
所成角的大小.
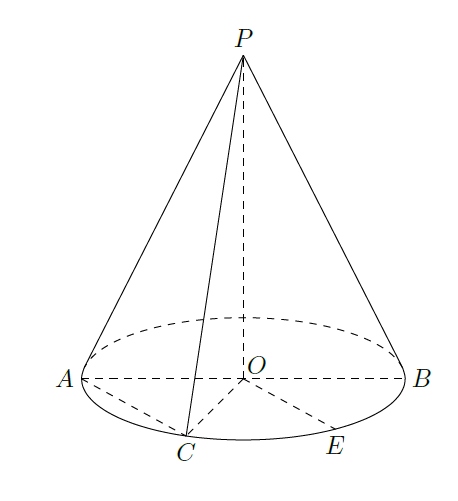
来源:2015年全国普通高等学校招生统一考试文科数学
已知函数
,其中
为实数.
(1)根据
的不同取值,判断函数
的奇偶性,并说明理由;
(2)若
,判断函数
在
上的单调性,并说明理由.
来源:2015年全国普通高等学校招生统一考试文科数学
如图,
三地有直道相通,
千米,
千米,
千米.现甲、乙两警员同时从
地出发匀速前往
地,经过
小时,他们之间的距离为
(单位:千米).甲的路线是
,速度为5千米/小时,乙的路线是
,速度为8千米/小时.乙到达
地后原地等待.设
时乙到达
地.
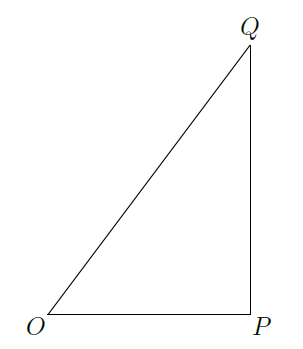
(1)求
与
的值;
(2)已知警员的对讲机的有效通话距离是3千米.当
时,求
的表达式,并判断
在
上得最大值是否超过3?说明理由.
来源:2015年全国普通高等学校招生统一考试文科数学
已知椭圆
,过原点的两条直线
和
分别于椭圆交于
、
和
、
,设
的面积为
.
(1)设
,
,用
、
的坐标表示点
到直线
的距离,并证明
;
(2)设
,
,
,求
的值;
(3)设
与
的斜率之积为
,求
的值,使得无论
与
如何变动,面积
保持不变.
来源:2015年全国普通高等学校招生统一考试文科数学
 粤公网安备 44130202000953号
粤公网安备 44130202000953号