高中数学圆锥曲线与方程试题

已知抛物线方程 $y^2=4x$ ， $F$ 为焦点， $P$ 为抛物线准线上一点， $Q$ 为线段 $\mathit{PF}$ 与抛物线的交点，定义： $d\left(P\right)=\frac{\left|\mathit{PF}\right|}{\left|\mathit{FQ}\right|}$ ．

（1）当 $P(-1,-\frac{8}{3})$ 时，求 $d\left(P\right)$ ；

（2）证明：存在常数 $a$ ，使得 $2d\left(P\right)=\left|\mathit{PF}\right|+a$ ；

（3） $P_1$ ， $P_2$ ， $P_3$ 为抛物线准线上三点，且 $\left|P_1{P}_2\right|=\left|P_2{P}_3\right|$ ，判断 $d\left(P_1\right)+d\left(P_3\right)$ 与 $2d\left(P_2\right)$ 的关系．

在椭圆 $\frac{x^2}{4}+\frac{y^2}{2}=1$ 上任意一点 $P$ ， $Q$ 与 $P$ 关于 $x$ 轴对称，若有 $\overrightarrow{F_{1}P}·\overrightarrow{F_{2}P}\le 1$ ，则 $\overrightarrow{F_{1}P}$ 与 $\overrightarrow{F_{2}Q}$ 的夹角范围为________．

设椭圆 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左焦点为 $F$，上顶点为 $B$．已知椭圆的短轴长为4，离心率为 $\frac{\sqrt{5}}{5}$．

（Ⅰ）求椭圆的方程；

（Ⅱ）设点 $P$在椭圆上，且异于椭圆的上、下顶点，点 $M$为直线 $\mathit{PB}$与 $x$轴的交点，点 $N$在 $y$轴的负半轴上．若 $\left|\mathit{ON}\right|=\left|\mathit{OF}\right|\mathit{}$（ $O$为原点），且 $\mathit{OP}\perp \mathit{MN}$，求直线 $\mathit{PB}$的斜率．

已知抛物线 $y^2=4x$ 的焦点为 $F$ ，准线为 $l$ ，若 $l$ 与双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$ 的两条渐近线分别交于点 和点 ，且 $\left|\mathit{AB}\right|=4\left|\mathit{OF}\right|$ （ 为原点），则双曲线的离心率为（ ）

A．

$\sqrt{2}$

B．

$\sqrt{3}$

C．

$2$

D．

$\sqrt{5}$

已知椭圆 $C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ 的右焦点为 $(1,0)$ ，且经过点 $A(0,1)$ ．

（Ⅰ）求椭圆 C的方程；

（Ⅱ）设 O为原点，直线 $l:y=\mathit{kx}+t(t\ne \pm 1)$ 与椭圆 C交于两个不同点 P， Q，直线 $\mathit{AP}$ 与 x轴交于点 M，直线 $\mathit{AQ}$ 与 x轴交于点 N，若 $\left|\mathit{OM}\right|·\left|\mathit{ON}\right|=2$ ，求证：直线 l经过定点．

设抛物线 $y^2=4x$ 的焦点为 $F$，准线为 $l$．则以 $F$为圆心，且与 $l$相切的圆的方程为__________．

已知双曲线 $\frac{x^2}{a^2}-y^2=1\left(a>0\right)$ 的离心率是 $\sqrt{5}$ ，则 $a=$ （ ）

A．

$\sqrt{6}$

B．

4

C．

2

D．

$\frac{1}{2}$

在平面直角坐标系 $\mathit{xOy}$ 中，椭圆 $E：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$ 的离心率为 $\frac{\sqrt{2}}{2}$ ，焦距为2．

（Ⅰ）求椭圆E的方程．

（Ⅱ）如图，该直线 $l：y=k_{1}x﹣\frac{\sqrt{3}}{2}$ 交椭圆E于A，B两点，C是椭圆E上的一点，直线OC的斜率为 $k_2$ ， 且看 $k_1{k}_2=\frac{\sqrt{2}}{4}$ ，M是线段OC延长线上一点，且 $\left|\mathit{MC}\right|：\left|\mathit{AB}\right|=2：3$ ，⊙M的半径为 $\left|\mathit{MC}\right|$ ，OS，OT是⊙M的两条切线，切点分别为S，T，求 $\angle \mathit{SOT}$ 的最大值，并求取得最大值时直线l的斜率．

在平面直角坐标系 $\mathit{xOy}$ 中，双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$ 的右支与焦点为F的抛物线 $x^2=2\mathit{py}\left(p＞0\right)$ 交于A，B两点，若 $\left|\mathit{AF}\right|+\left|\mathit{BF}\right|=4\left|\mathit{OF}\right|$ ，则该双曲线的渐近线方程为________．

已知椭圆 C： $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ ， $（a>b>0）$ 的左、右顶点分别为 $A_1$ ， $A_2$ ，且以线 $A_1{A}_2$ 为直径的圆与直线 $\mathit{bx}-\mathit{ay}+2\mathit{ab}=0$ 相切，则 C的离心率为（ ）

A．

$\frac{\sqrt{6}}{3}$

B．

$\frac{\sqrt{3}}{3}$

C．

$\frac{\sqrt{2}}{3}$

D．

$\frac{1}{3}$

如图，在平面直角坐标系xOy中，椭圆C: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的焦点为F ₁（-1、0），F ₂（1，0）．过F ₂作x轴的垂线l ，在x轴的上方，l与圆F ₂: ${(x-1)}^2+y^2=4a^2$ 交于点A ，与椭圆C交于点D.连结AF ₁并延长交圆F ₂于点B ，连结BF ₂交椭圆C于点E ，连结DF ₁．已知DF ₁= $\frac{5}{2}$ ．

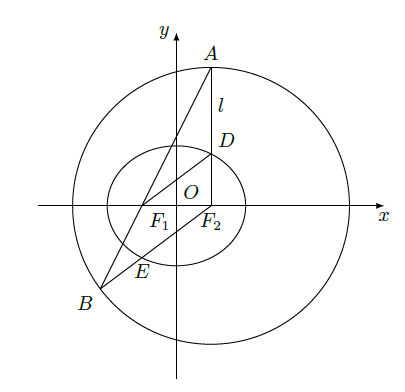
（1）求椭圆 C的标准方程；

（2）求点 E的坐标．

在平面直角坐标系 $\mathit{xOy}$ 中，若双曲线 $x^2-\frac{y^2}{b^2}=1(b>0)$ 经过点（3，4)，则该双曲线的渐近线方程是________.