2002年8月北京召开的国际数学家大会会徽如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是 ,小正方形的面积是 ,直角三角形的较长直角边为 ,较短直角边为 ,则 的值为( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在单位正方形组成的网格图中标出了 四条线段,其中能构成一个直角三角形三边的线段是( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中,点 在 边上,已知 ,且 ,则 为( )

| A. |
锐角三角形 |
B. |
直角三角形 |
C. |
钝角三角形 |
D. |
无法确定 |
已知 均为质数,但满足 ,则以 为边长的三角形是( )
| A. |
锐角三角形 |
B. |
直角三角形 |
C. |
钝角三角形 |
D. |
等腰三角形 |
恩施州自然风光无限,特别是以“雄、奇、秀、幽、险”著称于世.著名的恩施大峡谷 和世界级自然保护区星斗山(B)位于笔直的沪渝高速公路 同侧, 到直线 的距离分别为 和 ,要在沪渝高速公路旁修建一服务区 ,向 两景区运送游客.小民设计了两种方案.图①是方案一的示意图( 与直线 垂直,垂足为 到 的距离之和 ;图②是方案二的示意图(点 关于直线 的对称点是 ,连接 交直线 于点 到 的距离之和 .
(1)求 ,并比较它们的大小;
(2)请你说明 的值为最小;
(3)拟建的恩施到张家界高速公路 与沪渝高速公路垂直,建立如图③所示的直角坐标系, 到直线 的距离为 ,请你在 旁和 旁各修建一服务区 ,使 组成的四边形的周长最小,并求出这个最小值.

如图。(1)如图①以 的边 为边分别向外作正方形 和正方形 ,连接 ,试判断 与 面积之间的关系,并说明理由.
(2)园林小路,曲径通幽,如图②所示。小路由白色的正方形大理石和黑色的三角形大理石铺成.已知中间的所有正方形的面积之和是 ,内圈的所有三角形的面积之和是 ,这条小路一共占地多少 ?

如图, 三个村庄在同一条东西方向的公路沿线上, , ,在 村的正北方有一个 村,测得 ,今将 区域规划为开发区,除其中 的水塘外,均作为建筑及绿化用地,试求这个开发区的建筑及绿化用地的面积是多少?

如图, ,过点 作 且 ,得 ;再过点 作 且 ,得 ;又过 作 且 ,得 ,依此法继续下去,得 _____.

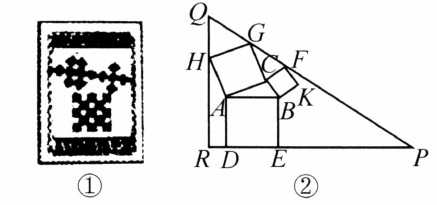
勾股定理有着悠久的历史,它曾引起很多人的兴趣.1955年希腊发行了一枚以勾股图为背景的邮票(如图①.所谓勾股图是指以直角三角形的三边为边向外作正方形构成的图形。它可以验证勾股定理.在图②的勾股图中,已知 .作 使得 ,点 在边 上,点 在边 上,点 在边 上,那么 的周长等于_____.
已知三角形相邻两边长分别为 和 ,第三边上的高为 ,则此三角形的面积为_____ .
如图,一只小猫沿着斜立在墙角的木板往上爬,木板底端距离墙角 ,当小猫从木板底端爬到顶端时,木板底端向左滑动了 ,木板顶端向下滑了 ,则小猫在木板上爬动了_____ .

如图是一种“羊头”形图案。其作法是:从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②’,…,依此类推,若正方形①的边长为 ,则正方形⑦的边长为_____ .
