已知二次函数y=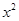 +bx+c的图象如图所示,它与x轴的一个交点的坐标为(-1,0),与y轴的交点坐标为(0,-3).
+bx+c的图象如图所示,它与x轴的一个交点的坐标为(-1,0),与y轴的交点坐标为(0,-3).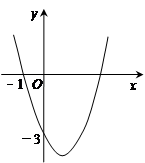
(1)求此二次函数的解析式;
(2)求此二次函数的图象与x轴的另一个交点的坐标;
(3)根据图象回答:当x取何值时,y<0?
(本题8分)
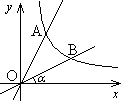
如图,直线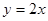 与反比例函数
与反比例函数 (
(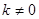 ,
,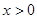 )的图象交于点A(1,
)的图象交于点A(1, ),B是反比例函数图象上一点,直线OB与
),B是反比例函数图象上一点,直线OB与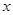 轴的夹角为
轴的夹角为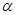 ,
,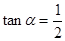 。
。
(1)求 的值;
的值;
(2)求点B的坐标;
(3)设点P(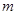 ,0),使△PAB的面积为2,求
,0),使△PAB的面积为2,求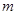 的值。
的值。
(本题8分)舟山市2010~2014年社会消费品零售总额及增速统计图如下:
请根据图中信息,解答下列问题:
(1)求舟山市2010~2014年社会消费品零售总额增速这组数据的中位数;
(2)求舟山市2010~2014年社会消费品零售总额这组数据的平均数;
(3)用适当的方法预测舟山市2015年社会消费品零售总额(只要求列式说明,不必计算出结果)。
如图,已知四边形ABCD是平行四边形,AD与△ABC的外接圆⊙O恰好相切于点A,边CD与⊙O相交于点E,连接AE,BE.
(1)求证:AB=AC;
(2)若过点A作AH⊥BE于H,求证:BH=CE+EH.
如图,在平面直角坐标系xOy中,直线l⊥y轴于点B(0,﹣2),A为OB的中点,以A为顶点的抛物线 与x轴交于C、D两点,且CD=4,点P为抛物线上的一个动点,以P为圆心,PO为半径画圆.
与x轴交于C、D两点,且CD=4,点P为抛物线上的一个动点,以P为圆心,PO为半径画圆.
(1)求抛物线的解析式;
(2)若⊙P与y轴的另一交点为E,且OE=2,求点P的坐标;
(3)判断直线l与⊙P的位置关系,并说明理由.
如图,在平面直角坐标系中,抛物线 (
( )与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,点A的坐标为(4,0),抛物线的对称轴是直线
)与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,点A的坐标为(4,0),抛物线的对称轴是直线 .
.
(1)求抛物线的解析式;
(2)M为第一象限内的抛物线上的一个点,过点M作MG⊥x轴于点G,交AC于点H,当线段CM=CH时,求点M的坐标;
(3)在(2)的条件下,将线段MG绕点G顺时针旋转一个角α(0°<α<90°),在旋转过程中,设线段MG与抛物线交于点N,在线段GA上是否存在点P,使得以P、N、G为顶点的三角形与△ABC相似?如果存在,请求出点P的坐标;如果不存在,请说明理由.
如图,AH是⊙O的直径,AE平分∠FAH,交⊙O于点E,过点E的直线FG⊥AF,垂足为F,B为直径OH上一点,点E、F分别在矩形ABCD的边BC和CD上.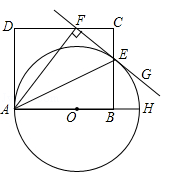
(1)求证:直线FG是⊙O的切线;
(2)若CD=10,EB=5,求⊙O的直径.
(本题12分)如图①所示,在正方形ABCD中,M是AB的中点,E是AB的延长线上一点,MN⊥DM,且交∠CBE的平分线于点N.
(1)求证:MD=MN;
(2)若将上述条件中“M是AB的中点”改成“M是AB上任意一点”,其余条件不变,如图②所示,则结论“MD=MN”还成立吗?若成立,给出证明;若不成立,请说明理由.
(本题13分)已知反比例函数y= (x>0)的图象经过点A(2,a)(a>0),过点A作AB⊥x轴,垂足为点B,将线段AB沿x轴正方向平移,与反比例函数y=
(x>0)的图象经过点A(2,a)(a>0),过点A作AB⊥x轴,垂足为点B,将线段AB沿x轴正方向平移,与反比例函数y= (x>0)的图象相交于点F(p,q).
(x>0)的图象相交于点F(p,q).
(1)当F点恰好为线段的中点时,求直线AF的解析式 (用含a的代数式表示);
(2)若直线AF分别与x轴、y轴交于点M、N,当q=-a2+5a时,令S=S△ANO+S△MFO(其中O是原点),求S的取值范围.
(本题12分)邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作:在余下的四边形纸片中再剪去一个菱形,又剩下一个四边形,称为第二次操作;…依次类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图1,▱ABCD中,若AB=1,BC=2,则▱ABCD为1阶准菱形.
(1)判断与推理: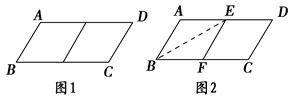
①邻边长分别为2和3的平行四边形是________阶准菱形;
②小明为了剪去一个菱形,进行了如下操作:如图2,把▱ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F,得到四边形ABFE.请证明四边形ABFE是菱形.
(2)操作、探究与计算:
①已知▱ABCD的邻边长分别为1,a(a>1),且是3阶准菱形,请画出▱ABCD及裁剪线的示意图,并在图形下方写出a的值;
②已知▱ABCD的邻边长分别为a,b(a>b),满足a=6b+r,b=5r,请写出▱ABCD是几阶准菱形.
(本题10分)如图,E为正方形ABCD对角线BD上的一点,且BE=BC=1.
(1)求∠DCE的度数;
(2)点P在EC上,作PM⊥BD于M,PN⊥BC于N,求PM+PN的值.
(本题13分)已知:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.
(1)如图1,当点D在线段BC上时,求证:①BD⊥CF.②CF=BC﹣CD.
(2)如图2,当点D在线段BC的延长线上时,其它条件不变,请直接写出CF、BC、CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:①请直接写出CF、BC、CD三条线段之间的关系.②若连接正方形对角线AE、DF,交点为O,连接OC,探究△AOC的形状,并说明理由.
(本题12分)某景区内的环形路是边长为800米的正方形ABCD,如图1和图2.现有1号、2号两游览车分别从出口A和景点C同时出发,1号车顺时针、2号车逆时针沿环形路连续循环行驶.供游客随时免费乘车(上、下车的时间忽略不计),两车速度均为200米/分.
探究
设行驶时间为t分.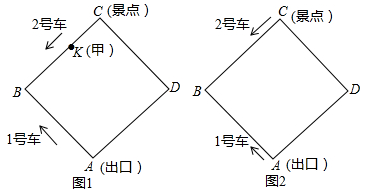
(1)当0≤t≤8时,分别写出1号车、2号车在左半环线离出口A的路程y1,y2(米)与t的函数关系式,并求出当两车相距的路程是400米时t的值;
(2)t为何值时,1号车第三次恰好经过景点C?并直接写出这一段时间内它与2号车相遇过的次数.
发现
如图2,游客甲在BC上的一点K(不与点B,C重合)处候车,准备乘车到出口A.设CK=x米.
情况一:若他刚好错过2号车,便搭乘即将到来的1号车;
情况二:若他刚好错过1号车,便搭乘即将到来的2号车.
比较哪种情况用时较多.(含候车时间)
决策
已知游客乙在DA上从D向出口A走去,步行的速度是50米/分.当行进到DA上一点P(不与点D,A重合)时,刚好与2号车迎面相遇.
(1)他发现,乘1号车会比乘2号车到出口A用时少,请你简要说明理由;
(2)设PA=s(0<s<800)米.若他想尽快到达出口A,根据s的大小,在等候乘1号车还是步行这两种方式中,他该如何选择?