初中数学解答题

如图，在平行四边形ABCD中，AE⊥BC于E，AF⊥CD于F，BD分别与AE、AF相交于G、H．

（1）在图中找出与△ABE相似的三角形，并说明理由；
（2）若AG=AH，求证：四边形ABCD是菱形．

在拖拉机油箱中，盛满56千克油，拖拉机工作时，每小时平均耗油6千克，求邮箱里剩下Q（千克）与拖拉机的工作时间t（小时）之间的函数关系式.

已知一次函数的图象a过点M（－1，－4.5），N（1，－1.5）
（1）求此函数解析式，并画出图象；
（2）求出此函数图象与x轴、y轴的交点A、B的坐标；
（3）若直线a与b相交于点P（4，m），a、b与x轴围成的△PAC的面积为6，求出点C的坐标．

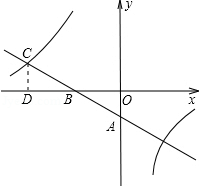
如图，一次函数y=kx+b的图象与坐标轴分别交于A，B两点，与反比例函数y=的图象在第二象限的交点为C，CD⊥x轴，垂足为D，若OB=2，OD=4，△AOB的面积为1．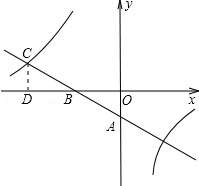

（1）求一次函数与反比例的解析式；
（2）直接写出当x＜0时，kx+b﹣＞0的解集．

解方程：

如图1，在平面直角坐标系中，为坐标原点.直线与抛物线同时经过.

（1）求的值.
（2）点是二次函数图象上一点，(点在下方)，过作轴，与交于点，与轴交于点.求的最大值.
（3）在（2）的条件下，是否存在点,使和 相似？若存在，求出点坐标，不存在，说明理由.

解下列方程
（1） （2）

（本题满分8分，每小题4分）
（1） 计算：；（2） 求中x的值．

如图，点A、F、C、D在同一直线上，点B和点E分别在直线AD的两侧，且AB=DE，∠A=∠D，AF=DC．
求证：△ABC≌△DEF;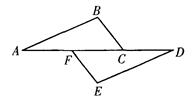

世界上最高的山峰是珠穆朗玛峰，其海拔高度是8844M，吐鲁番盆地的海拔高度大约是-155M。两处高度相差多少米﹖

（本题8分）在如图所示的方格纸中，每个小方格都是边长为1个单位的正方形，△ABO的三个顶点都在格点上．

（1）以O为原点建立直角坐标系，点B的坐标为（－3，1），则点A的坐标为；
（2）画出△ABO绕点O顺时针旋转90°后的△OA₁B₁，并求线段OA扫过的面积．

如图，四边形ABCD中，AC平分∠DAB，∠ADC=∠ACB=90°，E为AB的中点，

（1）求证：AC²=AB•AD；
（2）求证：CE∥AD；
（3）若AD=4，AB=6，求的值．

如图所示，点D在⊙O的直径AB的延长线上，点C在⊙O上，且AC=CD，∠ACD=．

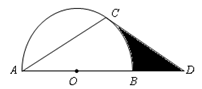
（1）求证：CD是⊙O的切线；
（2）若⊙O的半径为2，求图中阴影部分的面积．

解下列方程（每小题4分，共8分）
（1）（用配方法）
（2）

解方程：．