下列函数：①
；②
；③
；④
，y随x的增大而减小的函数有（ ）
| A．1个 | B．2个 | C．3个 | D．4个 |
如图，正比例函数
与反比例函数
相交于A、B点．已知点A的坐标为A（4，n），BD⊥x轴于点D，且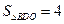
．过点A的一次函数
与反比例函数的图象交于另一点C，与x轴交于点E（5，0）．
（1）求正比例函数
、反比例函数
和一次函数
的解析式；
（2）结合图象，求出当
时
的取值范围．
如图．在直角坐标系中，矩形ABC0的边OA在x轴上，边0C在y轴上，点B的坐标为（1，3），将矩形沿对角线AC翻折，B点落在D点的位置，且AD交y轴于点E．那么点D的坐标为（ ）
A． |
B． |
C． |
D． |
将一张矩形纸片沿对角线剪开(如图1)，得到两张三角形纸片
、
(如
图2)，量得他们的斜边长为 6cm，较小锐角为30° ，再将这两张三角纸片摆成如图3的形状，且点 A、C、E、F 在同一条直线上，点 C 与点 E 重合， 保持不动，OB 为的中线，现对纸片进行如下操作时遇到了三个问题，请你帮助解决．
(1)将图3中的沿CA向右平移，直到两个三角形完全重合为止．设平移距离 CE 为 x(即 CE 的长)，求平移过程中，与
重叠部分的面积 S 与 x 的函数关系式，以及自变量的取值范围；
(2) 平移到 E 与O 重合时(如图4)，将绕点 O 顺时针旋转，旋转过程中的斜边 EF交的 BC 边于 G，求点 C、O、G构成等腰三角形时，
的面积；
(3)在(2)的旋转过程中， 的边 DE，EF分别交线段BC于点 G、H(不与端点重合)．求旋转角
为多少度时，线段BH、GH、CG之间满足 , 
请说明理由．
在同一直角坐标系中，正比例函数 的图象与反比例函数 的图象有公共点，则 0（填"＞"、"="或"＜"）.
某同学从家里出发，骑自行车上学时，速度v（米/秒）与时间t（秒）的关系如图a，A（10，5），B（130，5），C（135，0）.
（1）求该同学骑自行车上学途中的速度v与时间t的函数关系式；
（2）计算该同学从家到学校的路程（提示：在OA和BC段的运动过程中的平均速度分别等于它们中点时刻的速度，路程＝平均速度×时间）；
（3）如图b，直线x＝t（0≤t≤135），与图a的图象相交于P、Q，用字母S表示图中阴影部分面积，试求S与t的函数关系式；
（4）由（2）（3），直接猜出在t时刻，该同学离开家所超过的路程与此时S的数量关系.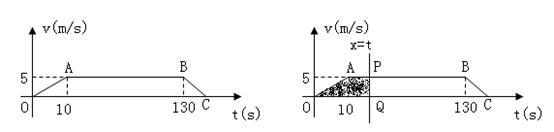
图a 图b
在一条直线上依次有A、B、C三个港口，甲、乙两船同时分别从A、B港口出发，沿直线匀速驶向C港，最终达到C港．设甲、乙两船行驶x（h）后，与B港的距离分别为
、
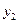（km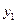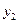），、与x的函数关系如图所示．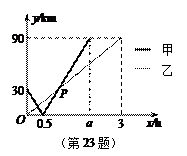
（1）填空：A、C两港口间的距离为 km，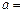
；
（2）求图中点P的坐标，并解释该点坐标所表示的实际意义；
（3）若两船的距离不超过10 km时能够相互望见，求甲、乙两船可以相互望见时x的取值范围．
函数y＝k(x－1)的图象向左平移一个单位后与反比例函数y＝
的图象的交点为A、B，若A点坐标为(1，2)，则B点的坐标为___▲___．
若把函数y=x的图象用E（x，x）记，函数y=2x+1的图象用E（x，2x+1）记，……则E（x，
）可以由E（x，
）怎样平移得到？
| A．向上平移１个单位 | B．向下平移１个单位 |
| C．向左平移１个单位 | D．向右平移１个单位 |
某服装厂承揽一项生产夏凉小衫1600件的任务，计划用t天完成．
（1）写出每天生产夏凉小衫w（件）与生产时间t（天）（t＞4）之间的函数关系式;
（2）由于气温提前升高，商家与服装厂商议调整计划，决定提前4天交货，那么服装厂每天要多做多少件夏凉小衫才能完成任务？
●探究 (1) 在图1中，已知线段AB，CD，其中点分别为E，F．
①若A (-1，0)， B (3，0)，则E点坐标为__________；
②若C (-2，2)， D (-2，-1)，则F点坐标为__________；
(2)在图2中，已知线段AB的端点坐标为A(a，b) ，B(c，d)，求出图中AB中点D的坐标（用含a，b，c，d的代数式表示），并给出求解过程．
●归纳 无论线段AB处于直角坐标系中的哪个位置，当其端点坐标为A(a，b)，B(c，d)， AB中点为D(x，y) 时，x=_________，y=___________．（不必证明）
●运用 在图3中，一次函数
与反比例函数
的图象交点为A，B．
①求出交点A，B的坐标；
②若以A，O，B，P为顶点的四边形是平行四边形，请利用上面的结论求出顶点P的坐标．
如图，是张老师出门散步时离家的距离
与时间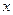
之间的函数关系的图象，若用黑点表示张老师家的位置，则张老师散步行走的路线可能是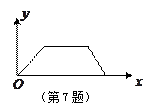
某洗衣机在洗涤衣服时经历了注水、清洗、排水三个连续过程（工作前洗衣机内无水），在这三个过程中洗衣机内水量y（升）与时间x之间的函数关系对应的图象大致为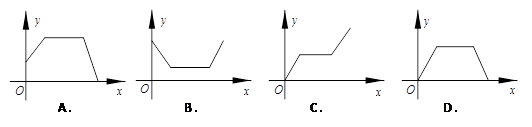
某校准备在甲、乙两家公司为毕业班学生制作一批纪念册．甲公司提出：每册收材料费5元，另收设计费1500元；乙公司提出：每册收材料费8元，不收设计费．
（1）设纪念册的册数为x，甲公司收费用
表示，乙公司收费用
表示，分别写出两家公司的收费与纪念册册数的关系；
（2）当纪念册的册数是多少时，两家公司的收费是一样的？
（3）如果学校派你去甲、乙两家公司订做纪念册，你会选择哪家公司？（就纪念册的册数讨论）
若正比例函数的图象经过点（
，2），则这个图象必经过点（ ）．
| A．（1，2） | B．（， ） |
C．（2，） |
D．（1，） |
粤公网安备 44130202000953号