每位同学都能感受到日出时美丽的景色.右图是一位同学从照片上剪切下来的画面,“图上”太阳与海平线交于A﹑B两点,他测得“图上”圆的半径为5厘米,AB=8厘米,若从目前太阳所处位置到太阳完全跳出海面的时间为16分钟,求“图上”太阳升起的速度.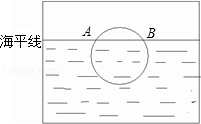
如图所示,AB是圆O的直径,以OA为直径的圆C与圆O的弦AD相交于点E.
求证:点E为AD的中点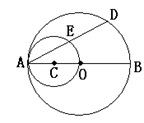
如图,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心 ,另一边所在直线与半圆相交于点
,另一边所在直线与半圆相交于点 ,量出半径
,量出半径 ,弦
,弦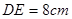 ,求这把直尺的宽度.
,求这把直尺的宽度.
如图所示,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D点,OC交AB于E点.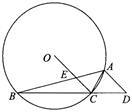
(1)求∠D的度数;
(2)求证:AC2=AD·CE.
如图,△ABC中,以AB为直径的⊙O交AC于点D,∠DBC=∠BAC.
(1)求证:BC是⊙O的切线.
(2)若⊙O的半径为2,∠BAC=30°,求图中阴影部分的面积.
如图,在Rt△ABC中,∠ACB=90°,AC=6,D为BC边上一点,CD=3,过A,C,D三点的⊙O与斜边AB交于点E,连结DE.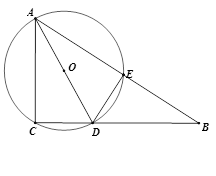
(1)求证:△BDE ∽△BAC;
(2)求△ACD外接圆的直径的长;
(3)若AD平分∠CAB,求出BD的长.
如图,⊙P与扇形OAB的半径OA、OB分别相切于点C、D,与弧AB相切于点E,已知OA=15cm,∠AOB=60°,求图中阴影部分的面积.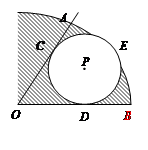
已知:如图,以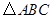 的边
的边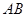 为直径的
为直径的 交边
交边 于点
于点 ,且过 点
,且过 点 的切线
的切线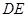 平分边
平分边 .
.
(1)求证: 是
是 的切线;
的切线;
(2)当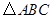 满足什么条件时,以点
满足什么条件时,以点 、
、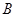 、
、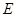 、
、 为顶点的四边形是平行四边形?请说明理由.
为顶点的四边形是平行四边形?请说明理由.
已知:如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点P,PD⊥AC于点D.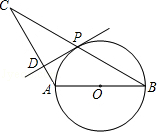
(1)求证:PD是⊙O的切线;
(2)若∠CAB=120°,AB=2,求BC的值.
如图,一条公路的转弯处是一段圆弧AB.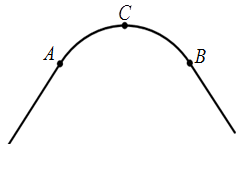
(1)用直尺和圆规作出弧AB所在圆的圆心O;(要求保留作图痕迹,不写作法)
(2)若弧AB的中点C到弦AB的距离为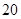 m,AB=80m,求弧AB所在圆的半径.
m,AB=80m,求弧AB所在圆的半径.
如图,已知⊙O的直径AB=12cm,AC是⊙O的弦,过点C作⊙O的切线交BA的延长线于点P,连接BC.
(1)求证:∠PCA=∠B;
(2)已知∠P=40°,点Q在优弧ABC上,从点A开始逆时针运动到点C停止(点Q与点C不重合),当△ABQ与△ABC的面积相等时,求动点Q所经过的弧长.
如图,已知AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,∠M=∠D.
(1)判断BC、MD的位置关系,并说明理由;
(2)若AE=16,BE=4,求线段CD的长;
(3)若MD恰好经过圆心O,求∠D的度数.