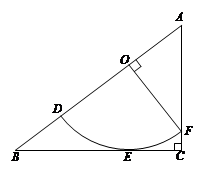初中数学圆幂定理计算题

如图，在△ABC中，∠ABC=90°，以AB的中点O为圆心，OA为半径的圆交AC于点D，E是BC的中点，连接DE，OE．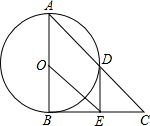

（1）判断DE与⊙O的位置关系，并说明理由；
（2）若cos∠BAD=，BE=，求OE的长．

如图，已知⊙O的直径AB与弦CD相交于点E，AB⊥CD，⊙O的切线BF与弦AD的延长线相交于点F．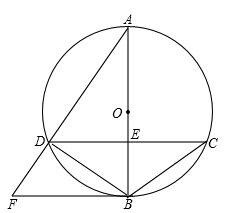

（1）求证：CD∥BF；
（2）若⊙O的半径为5，cos∠BCD=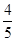，求线段AD的长．

如图在△ABC中，BE平分∠ABC，∠C=90°，D在AB边上，以DB为直径的半圆O经过点E交BC于点F．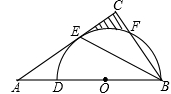

（1）求证：AC是⊙O的切线；
（2）已知sinA=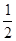，⊙O的半径为4，求图中阴影部分的面积．

如图，O是△ABC的内心，BO的延长线和△ABC的外接圆相交于D，连接DC、DA、OA、OC，四边形OADC为平行四边形。

（1）求证：△BOC≌△CDA
（2）若AB=2，求阴影部分的面积。

如图所示，点O在∠APB的平分线上，⊙O与PA相切于点C．

（1）求证：直线PB与⊙O相切
（2）PO的延长线与⊙O交于点E，若⊙O的半径为3，PC=4．求弦CE的长．

已知如图，以Rt△ABC的AC边为直径作⊙O交斜边AB于点E，连接EO并延长交BC的延长线于点D，点F为BC的中点，连接EF

（1）求证：EF是⊙O的切线；
（2）若⊙O的半径为3，∠EAC＝60°，求AD的长。

如图所示，AB是⊙O的直径，AD与⊙O相切于点A，DE与⊙O相切于点E，点C为DE延长线上一点，且CE=CB．

（1）求证：BC为⊙O的切线；
（2）若AB=4，AD=1，求线段CE的长．

如图，A为⊙O外一点，AB切⊙O于点B，AO交⊙O于C，CD⊥OB于E，交⊙O于点D，连接OD．若AB=12，AC=8．

（1）求OD的长； 
（2）求CD的长．

一扇形面积是3π，半径为3，则该扇形圆心角度数是（    ）

A．120°

B．90°

C．60°

D．

如图，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA＝∠CBD．

（1）求证：CD是⊙O的切线；
（2）若⊙O的半径为1，∠CBD＝30°，则图中阴影部分的面积；
（3）过点B作⊙O的切线交CD的延长线于点E若BC＝12，tan∠CDA＝，求BE的长．

如图，OC平分∠MON，点A在射线OC上，以点A为圆心，半径为2的⊙A与OM相切与点B，连接BA并延长交⊙A于点D，交ON于点E．

（1）求证：ON是⊙A的切线；
（2）若∠MON=60°，求图中阴影部分的面积．（结果保留π）

在中， 分别为所对的边，我们称关于的一元二次方程为“的☆方程”.根据规定解答下列问题：
（1）“的☆方程”的根的情况是   （填序号）；①有两个相等的实数根；②有两个不相等的实数根；③没有实数根.
（2）如图，为⊙的直径，点为⊙上的一点，的平分线交⊙于点，
求“的☆方程”的解；

（3）若是“的☆方程”的一个根，其中均为正整数，且，求：①求的值；②求“的☆方程”的另一个根.

如图，是半径为的上的定点，动点从出发，以的速度沿圆周逆时针运动，当点回到地立即停止运动．

（1）如果，求点运动的时间；
（2）如果点是延长线上的一点，，那么当点运动的时间为时，判断直线与的位置关系，并说明理由．

在△ABC中，∠C=90°，AC=6cm，BC=8cm，扇形ODF与BC边相切，切点是E，若FO⊥AB于点O．求扇形ODF的半径．

如图，在△ABC中，AB＝BC，以AB为直径的⊙O与AC交于点D，过D作DF⊥BC， 交AB的延长线于E，垂足为F．

(1)求证：直线DE是⊙O的切线；
(2)当AB＝5，AC＝8时，求cosE的值．