已知⊙O的半径是5,直线l是⊙O的切线,P是l上的任一点,那么下列结论正确的是
| A.0<OP<5 | B.OP=5 | C.OP>5 | D.OP≥5 |
如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B、 C两点,已知B(8,0),C(0,6),则⊙A的半径为( )

A.3 B.4 C.5 D.8
已知:如图,等边△ABC内接于⊙O,点P是劣弧 上的一点(端点除外),延长BP至D,使BD=AP,连接CD.
上的一点(端点除外),延长BP至D,使BD=AP,连接CD.
(1)若AP过圆心O,如图①,请你判断△PDC是什么三角形?并说明理由;
(2)若AP不过圆心O,如图②,△PDC又是什么三角形?为什么?
如图,AB是⊙O的直径,弦CD∥AB.若∠ABD=65°,则∠ADC= °.

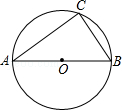
如图,C是以AB为直径的⊙O上一点,已知AB=5,BC=3,则圆心O到弦BC的距离是 .
以原点为圆心, 为半径的圆分别交
为半径的圆分别交 、
、 轴的正半轴于A、B两点,点P的坐标为
轴的正半轴于A、B两点,点P的坐标为 .
.
(1)如图一,动点Q从点B处出发,沿圆周按顺时针方向匀速运动一周,设经过的时间为 秒,当
秒,当 时,直线PQ恰好与⊙O第一次相切,连接OQ.求此时点Q的运动速度(结果保留
时,直线PQ恰好与⊙O第一次相切,连接OQ.求此时点Q的运动速度(结果保留 );
);
(2)若点Q按照⑴中的方向和速度继续运动,
①当 为何值时,以O、P、Q为顶点的三角形是直角三角形;
为何值时,以O、P、Q为顶点的三角形是直角三角形;
②在①的条件下,如果直线PQ与⊙O相交,请求出直线PQ被⊙O所截的弦长.


如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A、与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC、AD、BC之间的数量关系,并说明理由;
(3)若 ,求大圆与小圆围成的圆环的面积.(结果保留π)
,求大圆与小圆围成的圆环的面积.(结果保留π)
如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A.与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC,AD,BC之间的数量关系,并说明理由.
如果点O为△ABC的外心,∠BOC=70°,那么∠BAC等于 .
下列说法中正确的是( )
| A.平分弦的直径垂直于弦,并且平分弦所对的两条弧 |
| B.圆是轴对称图形,每一条直径都是它的对称轴 |
| C.弦的垂直平分线过圆心 |
| D.相等的圆心角所对的弧也相等 |
已知在△ABC中,∠B=90o,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.
(1)求证:AC·AD=AB·AE;
(2)如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.
如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为( )

| A.50° | B.80° | C.100° | D.130° |