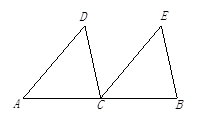初中数学三角形的五心解答题

一个多边形的内角和比它的外角和的3倍少180°，这个多边形的边数是多少？

一艘轮船由于风向原因先向正东方向航行了160km，然后向正北方向航行120km，这时它离出发点有多远？

如图，在四边形ABCD中，AD∥BC，∠C＝90°，BC＝16，DC＝12，AD＝21．动点P从点D出发，沿射线DA的方向以每秒2两个单位长的速度运动，动点Q从点C出发，在线段CB上以每秒1个单位长的速度向点B运动，点P，Q分别从点D，C同时出发，当点Q运动到点B时，点P随之停止运动．设运动的时间为t（秒）．

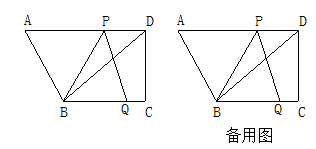
（1）请直接写出BD＝       ；AB＝       ；
（2）当t为何值时，以B，P，Q为顶点的三角形是等腰三角形？（求出一种得4分）
（3）是否存在时刻t，使得点P、Q关于BD对称，若存在，请你直接写出t的值，若不存在，请说明理由．

如图，直线l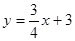：  交x、y轴分别为A、B两点，C点与A点关于y轴对称．动点P、Q分别在线段AC、AB上（点P不与点A、C重合），满足∠BPQ=∠BAO．

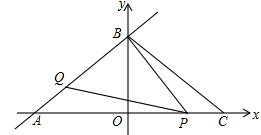
（1）点A坐标是__________，点B的坐标__________，BC=__________．
（2）当点P在什么位置时，△APQ≌△CBP，说明理由．
（3）当△PQB为等腰三角形时，求点P的坐标．

（本题14分）【问题探究】
（1）如图1，锐角△ABC中分别以AB、AC为边向外作等腰△ABE和等腰△ACD，使AE=AB，AD=AC，∠BAE=∠CAD，连接BD，CE，试猜想BD与CE的大小关系，并说明理由．
【深入探究】
（2）如图2，四边形ABCD中，AB=3cm，BC=1cm，∠ABC=∠ACD=∠ADC=45°，求BD的长（结果保留根号）．
（3）如图3，在（2）的条件下，当△ACD在线段AC的左侧时，求BD的长（结果保留根号）．

如图，已知AB=AC，AD=AE．求证：BD=CE．

（本题12分）已知：如图，∠ABC=∠ADC=90°，M，N分别是AC，BD的中点，求证：MN⊥BD．

用直尺和圆规在如图所示的数轴上作出的点．

（本题6分）某校把一块形状为直角三角形的废地开辟为生物园，如图所示，∠ACB=90°，AC=80米，BC=60米，若线段CD是一条小渠，且D点在边AB上，已知水渠的造价为10元/米，问D点在距A点多远处时，水渠的造价最低？最低造价是多少？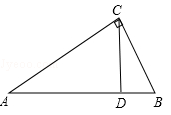

如图所示，在△ABC中，AB=AC，∠C=30°，AB⊥AD，AD=4cm，求BC的长．

如图，已知AB=CD，∠B=∠C，AC和BD相交于点O，E是AD的中点，连接OE．

（1）求证：△AOB≌△DOC；
（2）求∠AEO的度数．

一个零件的形状如图所示，按规定∠A=90°，∠C=25°，∠B=25°，检验员已量得∠BDC=150°，请问：这个零件合格吗？说明理由．

若△的三边满足，试判断△的形状．

如图，C为线段AB的中点，CD∥BE，CD＝BE．求证：AD∥CE．

如图，已知．求证：．