江苏扬州邗江美琪学校八年级上学期第二次月考数学卷
在实数1.732、 、-
、- 、
、 、
、 中,无理数有( )
中,无理数有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
2.0151精确到百分位是( )
| A.2.0 | B.2.01 | C.2.015 | D.2.02 |
下列各组数中互为相反数的一组是( )
A.-2与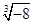 |
B.-2与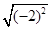 |
C.-2与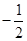 |
D.|-2|与2 |
与点P(a2+1,-a2-2)在同一个象限内的点是( )
| A.(3,2) | B.(-3,2) | C.(-3,-2) | D.(3,-2) |
点A(1,y1)、B(2,y2)都在一次函数y=-2x+3的图象上,则y1、y2的大小关系是( )
| A.y1>y2 | B.y1=y2 | C.y1<y2 | D.不确定 |
已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y=kx+k的图象经过的象限为( )
| A.二、三、四 | B.一、二、四 |
| C.一、三、四 | D.一、二、三 |
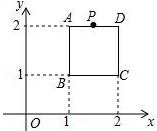
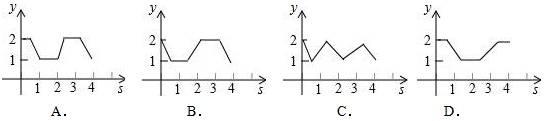
如图,在平面直角坐标系中,边长为1的正方形ABCD中,AD边的中点处有一动点P,动点P沿P→D→C→B→A→P运动一周,则P点的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是( )
全球七大洲的总面积约为149 480 000km2,对这个数据精确到百万位可表示为 km2.
若一次函数的图象过点(0,2),且函数y随自变量x的增大而增大,请写出一个符合要求的一次函数表达式: .
如图,已知函数y=x-2和y=-2x+1的图象交于点P,根据图象可得方程组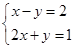 的解是 .
的解是 .
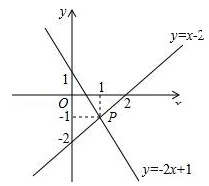
如图,点Q在直线y=-x上运动,点A的坐标为(1,0),当线段AQ最短时,点Q的坐标为 .

已知一次函数y=2x-3.
(1)当x=-2时,求y.
(2)当y=1时,求x.
(3)当-3<y<0时,求x的取值范围.
已知一次函数y=kx+b的图象经过两点A(1,1),B(2,-1),求这个函数的解析式.
已知(2a-1)的平方根是±3,(3a+b-1)的平方根是±4,求a+2b的平方根.
如图,平面直角坐标系中,每个小正方形边长都是1.

(1)按要求作图:
①△ABC关于x轴对称的图形△A1B1C1;
②将△A1B1C1向右平移7个单位得到△A2B2C2.
(2)回答下列问题:
①△A2B2C2中顶点B2坐标为 .
②若P(a,b)为△ABC边上一点,则按照(1)中①、②作图,点P对应的点P2的坐标为 .
阅读下面的文字,解答问题:
大家知道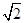 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此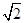 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用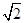 -1来表示
-1来表示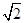 的小数部分,你同意小明的表示方法吗?
的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理,因为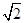 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:∵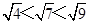 ,即
,即 ,
,
∴ 的整数部分为2,小数部分为(
的整数部分为2,小数部分为( -2).
-2).
请解答:(1)如果 的小数部分为a,
的小数部分为a,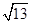 的整数部分为b,求a+b-
的整数部分为b,求a+b- 的值;
的值;
(2)已知:10+ =x+y,其中x是整数,且0<y<1,求x-y的相反数.
=x+y,其中x是整数,且0<y<1,求x-y的相反数.
已知一次函数y=kx+b的图象经过点(-2,4),且与正比例函数y=2x的图象平行.
(1)求一次函数y=kx+b的解析式;
(2)求一次函数y=kx+b的图象与坐标轴所围成的三角形的面积;
(3)若A(a,y1),B(a+b,y2)为一次函数y=kx+b的图象上两个点,试比较y1与y2的大小.
自2012年6月1日起,全国实施了阶梯电价.某省出台了阶梯电价方案:电价分“三档”收费,第一档为a度,居民用电量低于a度的部分,执行现行的标准电价(0.53元/度);第二档为a~b度,居民月用电量在a~b之间的部分,电价在一档电价的基础上提高0.05元/度;第三档为超过b度,居民月用电量高于b度的部分,电价在一档电价的基础上提高m元/度.实施阶梯电价后,月电费y(元)与月用电量x(度)之间的函数关系如图所示.
(1)求a,b,m的值;
(2)求y与x之间函数关系式,并写出自变量x的取值范围.
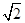
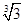
 = .
= . 的绝对值是 ,1+
的绝对值是 ,1+ 的相反数是 ,
的相反数是 , 的倒数是 .
的倒数是 .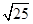 的算术平方根是 .绝对值最小的实数是 .
的算术平方根是 .绝对值最小的实数是 .
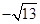 的点.
的点.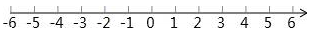
 x的图象交于点C,点C的横坐标为-3.
x的图象交于点C,点C的横坐标为-3.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号