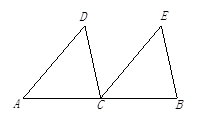如图,已知AB=CD,∠B=∠C,AC和BD相交于点O,E是AD的中点,连接OE.
(1)求证:△AOB≌△DOC;
(2)求∠AEO的度数.
如图,△ABD中,∠BAD=90°,AB=AD,△ACE中,∠CAE=90°,AC=AE.
(1)求证:DC=BE;
(2)试判断∠AFD和∠AFE的大小关系,并说明理由.
一个零件的形状如图所示,按规定∠A=90°,∠C=25°,∠B=25°,检验员已量得∠BDC=150°,请问:这个零件合格吗?说明理由.
如图,直线l: 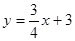 交x、y轴分别为A、B两点,C点与A点关于y轴对称.动点P、Q分别在线段AC、AB上(点P不与点A、C重合),满足∠BPQ=∠BAO.
交x、y轴分别为A、B两点,C点与A点关于y轴对称.动点P、Q分别在线段AC、AB上(点P不与点A、C重合),满足∠BPQ=∠BAO.
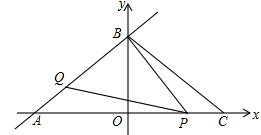
(1)点A坐标是__________,点B的坐标__________,BC=__________.
(2)当点P在什么位置时,△APQ≌△CBP,说明理由.
(3)当△PQB为等腰三角形时,求点P的坐标.
如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°.已知山坡AB的坡度为i=1︰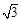 ,AB=10米,AE=15米.(i=1︰
,AB=10米,AE=15米.(i=1︰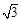 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据: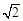 ≈1.414,
≈1.414,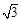 ≈1.732)
≈1.732)
如图,已知:EC=AC,∠BCE=∠DCA,∠A=∠E.求证:∠B=∠D.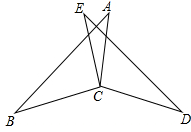
如图所示,成纪大道与天北高速在七里墩相交于点O,在∠AOB的内部有工厂C和D,现要建一个货场P,使P到OA和OB的距离相等,且使PC=PD,用尺规作出P点的位置.(不写作法,保留作图痕迹)
已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°.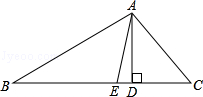
(1)求∠DAE的度数;
(2)试写出∠DAE与∠C﹣∠B有何关系?(不必证明)
已知:如图,∠C=90°,BC=AC,D、E分别在BC和AC上,且BD=CE,M是AB的中点.求证:DM=EM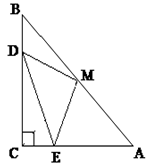
爱动脑筋的小明在学习了全等三角形和等腰三角形有关知识后作了如下探索:
(1)已知,如图,△ABC中,∠BAC是锐角,AB=AC,高AD、BG 所在的直线相交于点H, 且AG=BG,则AH和BC的关系是:_____________________;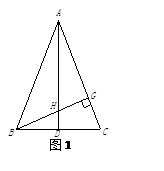

(2)若把(1)中的“∠BAC是锐角”改为“∠BAC是钝角”(如图2),其他条件都不变, AH和BC的关系是否仍然成立, 若成立,请在图2中用三角板和量角器画出完整的图形并证明;若不成立,请说明理由.
如图,C为线段AB的中点,CD∥BE,CD=BE.求证:AD∥CE.