初中数学一次函数的最值解答题

如图，已知二次函数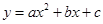的图象过A（2，0），B（0，﹣1）和C（4，5）三点．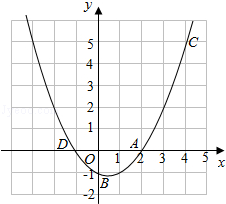

（1）求二次函数的解析式；
（2）设二次函数的图象与x轴的另一个交点为D，求点D的坐标；
（3）在同一坐标系中画出直线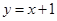，并写出当x在什么范围内时，一次函数的值大于二次函数的值．

如图，已知二次函数y=ax²+bx+c的图象过A（2，0），B（0，﹣1）和C（4，5）三点．

（1）求二次函数的解析式；
（2）设二次函数的图象与x轴的另一个交点为D，求点D的坐标；
（3）在同一坐标系中画出直线y=x+1，并写出当x在什么范围内时，一次函数的值大于二次函数的值．

2013年5月，长江三峡国际龙舟拉力赛揭开比赛帷幕．20日上午9时，参赛龙舟从起点同时出发．其中甲、乙两队在比赛时，路程y（千米）与时间x（小时）的函数关系如图所示．甲队在上午11时30分到达终点．

（1）哪个队先到达终点？乙队何时追上甲队？
（2）在比赛过程中，甲、乙两队何时相距最远？

明明乘出租车从游泳馆到翠岗小区，出租车行驶了4.5km。如果出租车的收费标准为：行驶路程不超过3km收费7元，超过3km的部分按每千米加1.8元收费。
（1）请帮明明用代数式表示出租车的收费m元与行驶路程skm（s>3）之间的关系；
（2）明明身上有10元钱，够不够付车费呢？说明理由。

如图，在平面直角坐标系中，直线y=0.5x+2与x轴、y轴分别交于A、B两点，以AB为边在第二象限内作正方形ABCD，过点D作DE⊥x轴，垂足为E.

（1）求点A、B的坐标，并求边AB的长；
（2）求点D的坐标；
（3）你能否在x轴上找一点M，使△MDB的周长最小？如果能，请求出M点的坐标；如果不能，说明理由.

已知一次函数y=kx+b的图像经过点（－1.－5），且与正比例函数y=x的图象相交于点（2，m）.
（1）求m的值；
（2）求一次函数y=kx+b的解析式；
（3）求这两个函数图像与x轴所围成的三角形面积.

某公司有A型产品40件，B型产品60件，分配给下属甲、乙两个商店销售，其中70件给甲店，30件给乙店，且都能卖完，两商店销售这两种产品每件的利润（元）如下表：

	A型利润	B型利润
甲店	200	170
乙店	160	150

 
（1）设分配给甲店A型产品x件，这件公司卖出这100件产品的总利润W（元），求W关于x的函数关系式，并求出x的取值范围；
（2）若要求总利润不低于17560元，有多少种不同分配方案，并将各种方案设计出来；
（3）为了促销，公司决定仅对甲店A型产品让利销售，每件让利a元，但让利后A型产品的每件利润仍高于甲店B型产品的每件利润.甲店的B型产品以及乙店的A、B型产品的每件利润不变，问该公司又如何设计分配方案，使总利润达到最大.

（本题12分）如图1，在长方形ABCD中，AB＝12cm，BC＝6cm，点P从A点出发，沿
A→B→C→D路线运动，到D点停止；点Q从D点出发，沿D→C→B→A运动，到A点停止．若点P、点Q同时出发，点P的速度为每秒1cm，点Q的速度为每秒2cm，a秒时点P、点Q同时改变速度，点P的速度变为每秒b（cm），点Q的速度变为每秒c（cm）．如图2是点P出发x秒后△APD的面积S₁（cm²）与x（秒）的函数关系图象；图3是点Q出发x秒后△AQD的面积S₂（cm²）与x（秒）的函数关系图象．根据图象：

（1）请直接写出a＝         、b＝         、c＝         ；
（2）设点P离开点A的运动路程为y₁（cm），点Q到点A还需要走的路程为y₂（cm），请分别写出改变速度后y₁、y₂与出发后的运动时间x（秒）的函数表达式，并求出P与Q相遇时x的值．

（本题10分）已知一次函数y＝kx＋b的图像经过点（－1，－2），且与正比例函数y＝x的图像相交于点（2，a）．
（1）求a、b、k的值；
（2）在图中画出这两个函数图像，并求这两个函数图像与x轴所围成的三角形面积．

如图，在平面直角坐标系xOy中，直线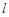与x轴交于点A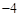（，），与y轴的正半轴交于点
B．点C在直线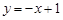上，且CA⊥x轴于点A．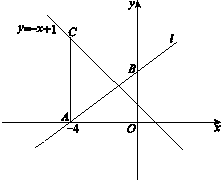

（1）求点C的坐标；
（2）若点D是OA的中点，点E是y轴上一个动点，当EC+ED最小时，求此时点E的坐标；
（3）若点A恰好在BC的垂直平分线上，点F在x轴上，且△ABF是以AB为腰的等腰三角形，请直接写出所有满足条件的点F的坐标．

如图，在平面直角坐标系xOy中，一次函数的图象经过点A（，），且与正比例函数的图象交于点B（，）．

（1）求的值及一次函数的解析式；
（2）若一次函数的图象与x轴交于点C，且正比例函数的图象向下平移m（m>0）个单位长度后经过点C，求m的值；
（3）直接写出关于x的不等式的解集．

如图，在平面直角坐标系中，一次函数的图象与y轴交于点A，与x轴交于点B，与反比例函数的图象分别交于点M，N，已知△AOB的面积为1，点M的纵坐标为2

（1）求一次函数和反比例函数的解析式；
（2）直接写出时x的取值范围．

如图，一次函数y=kx+2的图象与x轴交于点B，与反比例函数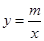的图象的一个交点为（2，3）．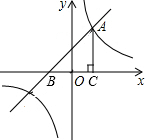

（1）分别求反比例函数和一次函数的表达式；
（2）过点A作AC⊥x轴，垂足为C，若点P在反比例函数图象上，且△PBC的面积等于18，请直接写出点P的坐标．

（12分如图，直线l₁与x轴、y轴分别交于A、B两点，直线l₂与直线l₁关于x轴对称，已知直线l₁的解析式为．

（1）求直线l₂的解析式；
（2）过A点在△ABC的外部作一条直线l₃，过点B作BE⊥l₃于E，过点C作CF⊥l₃于F，请画出图形并求证：BE+CF=EF；
（3）△ABC沿y轴向下平移，AB边交x轴于点P，过P点的直线与AC边的延长线相交于点Q，与y轴相交于点M，且BP=CQ，在△ABC平移的过程中，①OM为定值；②MC为定值．在这两个结论中，有且只有一个是正确的，请找出正确的结论，并求出其值．

某县为实现经济跨越，高度重视交通事业的发展．现有甲、乙两个工程队分别同时建筑两条水泥路面，所建路的长度y（m）与建筑的时间t（h）之间关系如下图所示，请根据图象提供的信息解答下列问题：

（1）乙队筑路到40m时，用了            h．筑路5h时，甲队比乙队多筑了          m．
（2）请你求出：
①甲队在≤≤的时段内，y与x的函数关系式；
②乙队在≤≤的时段内，y与x的函数关系式．
（3）筑路多长时间时，甲、乙两队筑路的长度相等．