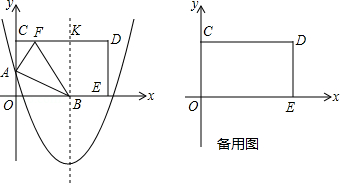
如图,在平面直角坐标系中,矩形
的顶点
和
分别在
轴的正半轴和
轴的正半轴上,
,
,抛物线
与
轴相交于点
,抛物线的对称轴与
轴相交于点
,与
交于点
.
(1)将矩形
沿
折叠,点
恰好落在边
上的点
处.
①点
的坐标为
、
,
的长是 ,
的长是 ;
②求点
的坐标;
③请直接写出抛物线的函数表达式;
(2)将矩形
沿着经过点
的直线折叠,点
恰好落在边
上的点
处,连接
,折痕与
相交于点
,点
是线段
上的一个动点(不与点
重合),连接
,
,过点
作
于点
,交
于点
,连接
,点
从点
开始沿线段
向点
运动,至与点
重合时停止,
和
的面积分别表示为
和
,在点
的运动过程中,
(即
与
的积)的值是否发生变化?若变化,请直接写出变化范围;若不变,请直接写出这个值.
温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.
 的图象与y轴交于点A,与x轴交于点B,与反比例函数
的图象与y轴交于点A,与x轴交于点B,与反比例函数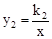 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐标为2
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐标为2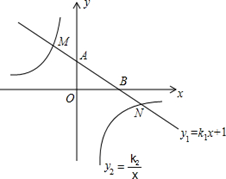
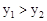 时x的取值范围.
时x的取值范围. 的图象与y轴交于点A,与x轴交于点B,与反比例函数
的图象与y轴交于点A,与x轴交于点B,与反比例函数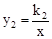 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐标为2
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐标为2
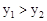 时x的取值范围.
时x的取值范围.