某中学以“我最喜爱的书籍”为主题，对学生最喜爱的书籍类型的情况进行了随机抽样调查（每位被调查者必须且只能选择最喜爱的一种书籍），并将调查结果绘制成如下的两幅不完整的统计图：
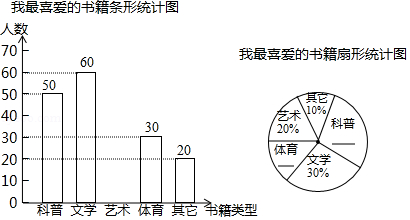
请根据图中提供的信息，回答下列问题：
（1）求本次被调查学生的人数；
（2）请将上面的两幅统计图补充完整；
（3）若从2名最喜爱文学书籍和2名最喜爱科普书籍的学生中随机抽取2人，请用列表或画树状图的方法求所抽取的两人恰好都是最喜爱文学书籍的概率．
相关试题
先化简，后求值，其中
．
=
=
=
.
中，
∥
，∠
°，且对角线
，试问：
与△
相似吗？请说明理由.
，
，请求出
的长．（本小题满分9分）已知：关于x的方程kx2-（3k-1）x+2（k-1）=0
（1）求证：无论k为何实数，方程总有实数根；
（2）若此方程有两个实数根x1，x2，且
，求k的值．
，在x=1﹑2 ﹑－
中选一个你喜欢的数代入计算。
推荐套卷
粤公网安备 44130202000953号