初中数学一次函数的最值解答题

某股份有限公司根据公司实际情况，对本公司职工实行内部医疗公积金制度，公司规定：
（一）每位职工在年初需缴纳医疗公积金m元；
（二）职工个人当年治病花费的医疗费年底按表1的办法分段处理：
表1

分段方式	处理办法
不超过150元（含150元）	全部由个人承担
超过150元，不超过10000元（不含150元，含10000元）的部分	个人承担n%，剩余部分由公司承担
超过10000元（不含10000元）的部分	全部由公司承担

 
设一职工当年治病花费的医疗费为x元，他个人实际承担的费用（包括医疗费个人承担的部分和缴纳的医疗公积金m元）为y元．
（1）由表1可知，当时，；那么，当时，y =   ；
（用含m、n、x的方式表示）
（2）该公司职工小红和大明2014年治病花费的医疗费和他们个人实际承担的费用如表2：

职工	治病花费的医疗费x（元）	个人实际承担的费用y（元）
小红	300	280
大明	500	320

 
请根据表2中的信息，求m、n的值，并求出当时，y关于x函数解析式；
（3）该公司职工个人一年因病实际承担的费用最多只需要多少元？

（本题10分）对于平面直角坐标系中的任意两点P₁（x₁,y₁），P₂（x₂,y₂），我们把|x₁－x₂|+|y₁－y₂|叫做P₁、P₂两点间的直角距离，记作d（P₁,P₂）．
 
（1）令P₀（2,－3），O为坐标原点，则d（O,P₀）＝       ；
（2）已知O为坐标原点，动点P（x,y）满足d（O,P）＝1，请写出x与y之间满足的关系式，并在所给的直角坐标系中画出所有符合条件的点P所组成的图形；
（3）设P₀（x₀,y₀）是一定点，Q（x,y）是直线y=ax+b上的动点，我们把d（P₀,Q）的最小值叫做P₀到直线y=ax+b的直角距离．若P（a,－3）到直线y=x＋1的直角距离为6，求a的值．

某乡组织20辆汽车装运A、B、C三个品种的苹果42吨到外地销售。按规定每辆车只装同一品种苹果，且必须装满。每一个品种苹果不少于2车。

苹果品种	A	B	C
每辆汽车运载量（吨）	2．2	2．1	2
每吨苹果获利（百元）	6	8	5

 
（1）设x辆车装运A种苹果，用y辆车装运B种苹果，根据上表提供的信息，求x与y间的函数关系式，并求x的取值范围；
（2）设此次外销活动的利润为 w （百元），求w与x的函数关系式以及最大利润，并写出相应的车辆分配方案。

一次函数 y=-x+5的图像与y=kx-1的图像都经过点（2，a）．
（1）求a和k的值．
（2）判断点（-1，1）是否在一次函数y=kx-1的图像上．

如图，在平面直角坐标系中，直线y=x+4分别交x轴，y轴于A，B两点，点C为OB的中点，点D在第二象限，且四边形AOCD为矩形．

（1）直接写出点A，B的坐标，并求直线AB与CD交点E的坐标；
（2）动点P从点C出发，沿线段CD以每秒1个单位长度的速度向终点D运动；同时，动点N从点A出发，沿线段AO以每秒1个单位长度的速度向终点O运动，过点P作PH⊥OA，垂足为H，连接NP．设点P的运动时间为t秒．
① 若△NPH的面积为1，求t的值；
② 点Q是点B关于点A的对称点，问BP+PH+HQ是否有最小值，如果有，求出相应的点P的坐标；如果没有，请说明理由．

（
知识迁移
当且时，因为≥,所以≥,
从而≥（当时取等号）.
记函数,由上述结论可知：当时,该函数有最小值为.
直接应用
已知函数与函数, 则当_________时,取得最小值为_________.
变形应用
已知函数与函数,求的最小值,并指出取得该最小值时相应的的值.
实际应用
已知某汽车的一次运输成本包含以下三个部分：一是固定费用,共元；二是燃油费,每千米为元；三是折旧费,它与路程的平方成正比,比例系数为.设该汽车一次运输的路程为千米,求当为多少时,该汽车平均每千米的运输成本最低？最低是多少元？

为奖励在演讲比赛中获奖的同学，班主任派学习委员小明为获奖同学买奖品，要求每人一件．小明到文具店看了商品后，决定奖品在钢笔和笔记本中选择．如果买4个笔记本和2支钢笔，则需86元；如果买3个笔记本和1支钢笔，则需57元．
（1）求购买每个笔记本和钢笔分别为多少元；
（2）售货员提示，买钢笔有优惠，具体方法是：如果买钢笔超过10支，那么超出部分可以享受8折优惠，若买x（x＞10）支钢笔需要花y元，请你求出y与x的函数关系式；
（3）在（2）的条件下，小明决定买同一种奖品，数量超过10个，请帮小明判断买哪种奖品省钱．

如图，一次函数y＝ax＋b的图象与反比例函数的图象相交于A，B两点，与y轴交于点C，与x轴交于点D，点D的坐标为（－2,0），点A的横坐标是2，tan∠CDO＝.

（1）求点A的坐标；
（2）求一次函数和反比例函数的解析式；
（3）求△AOB的面积．

从无锡供电公司获悉，现我市执行阶梯电价。居民月用电量分为三个档次，第一档230度及以内，维持现行电价标准即每度按0．53元收取；第二档为231度至400度，即每个月用电量超出230度不超过400度部分，按照每度0．58元收取；第三档为高于400度部分。，即超出400度部分，按照每度0．83元收取
请完成下列问题：
（1）如果该地区某户居民2014年8月用电310度，则该居民8月应付电费为     元．
（2）实行阶梯电价后，如果月用电量用x（度）表示，月支出电费用y（元）表示，小红、小明、小丽三人绘制了如下大致图像，你认为正确的是       ．

（3）小明同学家2014年11、12两月共用电460度，且11月份用电量少于12月份，他通过计算发现：他这两个月的电费比调整前多出了2．5元。你能求出他家11、12两月用电量分别是多少吗？

两会期间，环保问题受到与会代表的广泛关注．近期多地纯电动出租车正式上路运行，下表是普通燃油出租车和纯电动出租车的运价．

车型	起步公里数	起步价格	超出起步公里数后的单价
普通燃油型	3	9元＋2元（燃油附加费）	2．4元/公里
纯电动型	2．5	9元	2．9元/公里

 
设乘客打车的路程为x公里,乘坐普通燃油出租车及纯电动出租车所需费用分别为y₁、y₂元．
（1）直接写出y₁、y₂关于x的函数关系式，并注明对应的x的取值范围；
（2）在如下的同一个平面直角坐标系中，画出y₁、y₂关于x的函数图象；
（3）结合图象，求出当乘客打车的路程在什么范围内时，乘坐纯电动出租车更合算．

（本小题满分6分）在平面直角坐标系xOy中，直线y=kx+4（k≠0）与y轴交于点A.
（1）如图，直线y=－2x+1与直线y=kx+4（k≠0）交于点B，与y轴交于点C，点B的横坐标为-1.

①求点B的坐标及k的值；
②直线y=－2x+1、直线y=kx+4与y轴所围成的△ABC的面积等于               ；
（2）直线y=kx+4（k≠0）与x轴交于点E（,0）,若-2＜＜-1，求k的取值范围.

（本题6分）已知直线y=kx+b经过（—2，0）、（1，6），求不等式kx+b≥-x的解集.

如图，已知A（4，a）B（-2，-4）是一次函数y=kx+b的图像和反比例函数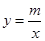的图像的交点．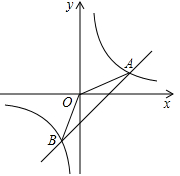

（1）求反比例函数和一次函数的解析式；
（2）根据图象直接写出：当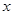取何值时，反比例函数的值大于一次函数的值．
（3）求ΔAOB的面积．

元旦期间，甲、乙两个家庭到300 km外的风景区“自驾游”，乙家庭由于要携带一些旅游用品，比甲家庭迟出发0．5 h（从甲家庭出发时开始计时），甲家庭开始出发时以60 km/h的速度行驶．途中的折线、线段分别表示甲、乙两个家庭所走的路程y_甲（km）、y_乙（km）与时间x（h）之间的函数关系对应图象，请根据图象所提供的信息解决下列问题：

（1）由于汽车发生故障，甲家庭在途中停留了      h；
（2）甲家庭到达风景区共花了多少时间；
（3）为了能互相照顾，甲、乙两个家庭在第一次相遇后约定两车的距离不超过15 km，请通过计算说明，按图所表示的走法是否符合约定．

【改编】如图，己知：反比例函数的图象与一次函数y=mx＋b的图象交于点A（1，4），点B（-4，n）．

（1）求一次函数和反比例函数的解析式；
（2）求△OAB的面积．
（3）在直线AB上是否存在点P,使得△AOP是以OP为腰的等腰三角形，若存在，直接写出点P的坐标，若不存在，说明理由．