初中数学一次函数的最值解答题

（本题8分）如图，L₁，L₂分别表示一种白炽灯和一种节能灯的费用y（费用=灯的售价+电费，单位：元）与照明时间x（h）的函数图像，

（1）根据图像分别求出L₁，L₂的函数关系式．
（2）当照明时间为多少时，两种灯的费用相等?
（3）假设两种灯的使用寿命都是2000h，照明效果一样．小亮房间计划照明2500h，他买了一个白炽灯和一个节能灯，请你帮他设计最省钱的用灯方法（直接给出答案，不必写出解答过程）．

“龟兔赛跑”的故事同学们都非常熟悉，图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系，请你根据图中给出的信息，解决下列问题．

（1）填空：折线OABC表示赛跑过程中          的路程与时间的关系，线段OD表示赛跑过程中          的路程与时间的关系．赛跑的全程是           米．
（2）兔子在起初每分钟跑         米，乌龟每分钟爬         米．
（3）乌龟用了           分钟追上了正在睡觉的兔子．
（4）兔子醒来，以48千米/时的速度跑向终点，结果还是比乌龟晚到了0．5分钟，请你算算兔子中间停下睡觉用了多少分钟？

在学习地理时，我们知道：“海拔越高，气温越低”，下表是海拔高度h（千米）与此高度处气温t（℃）的关系．

根据上表，回答以下问题．
（1）请写出气温t与海拔高度h的关系式；
（2）2014年3月8日，马航MH370航班失去联系，据报道称，马航MH370航班失去联系前飞行高度1066米，请计算在该海拔高度时的气温大约是多少？
（3）当气温是零下40℃时，其海拔高度是多少？

已知：如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，点P在BC上运动，点P不与点B，C重合，设PC=x，若用y表示△APB的面积，求y与x的函数关系式，并求自变量x的取值范围．

因南方旱情严重，乙水库的蓄水量以每天相同的速度持续减少．为缓解旱情，北方甲水库立即以管道运输的方式给予支援．下图是两水库的蓄水量y（万米3）与时间x（天）之间的函数图象．在单位时间内，甲 水库的放水量与乙水库的进水量相同（水在排放、接收以及输送过程中的损耗不计）．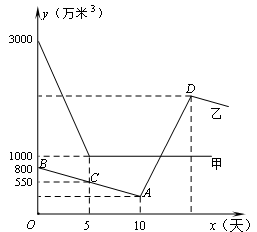

通过分析图象回答下列问题：
（1）甲水库每天的放水量是多少万立方米？
（2）在第几天时甲水库输出的水开始注入乙水库？此时乙水库的蓄水量为多少万立方米？
（3）求直线AD的解析式．

如图，直线y=mx与双曲线y=相交于A、B两点，A点的坐标为（1，2）

（1）求反比例函数的表达式
（2）根据图象直接写出当mx＞时，x的取值范围；
（3）计算线段AB的长．

如图，二次函数的图象与x轴交于A（﹣3，0）和B（1，0）两点，交y轴于点C（0，3），点C、D是二次函数图象上的一对对称点，一次函数的图象过点B、D．

（1）求二次函数的解析式；
（2）根据图象直接写出使一次函数值大于二次函数值的x的取值范围；
（3）若直线与y轴的交点为E，连结AD、AE，求△ADE的面积．

问题1：在图1中，已知线段AB，CD，它们的中点分别为E，F．
①若，，则点坐标为_____________；
②若，，则点坐标为____________；
问题2：在图2中，无论线段处于直角坐标系中的哪个位置，当其端点坐标为，，中
点为时，请直接写出点的坐标（____________，___________）；（用含、、、的式子表示）．
问题3：如图3，一次函数与反比例函数的图象交于、两点，若以、、、为顶
点的四边形是平行四边形，请直接写出顶点的坐标______________．

如图，直线AB过点A，且与y轴交于点B．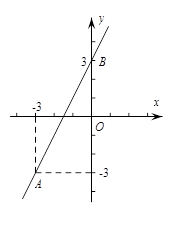

（1）求直线AB的解析式；
（2）若点P是直线AB上一点，且的半径为1，请直接写出与坐标轴相切时点P的坐标．

下面的图像反映的过程是：小明从家去超市买文具，又去书店购书，然后回家．其中x表示时间，y表示小明离他家的距离，若小明家、超市、书店在同一条直线上．
根据图像回答下列问题：

（1）超市离小明家多远，小明走到超市用了多少时间？
（2）超市离书店多远，小明在书店购书用了多少时间？
（3）书店离小明家多远，小明从书店走回家的平均速度是每分钟多少米？

为丰富群众的业余生活，我市准备组织篮球比赛，市体育局策划本次活动，在与单位协商团购票时推出两种方案．设购买门票数为x（张），总费用为y（元）．方案一：若单位赞助广告费8000元，则该单位所购门票的价格为每张50元；（总费用=广告赞助费+门票费）
方案二：直接购买门票方式如图所示．解答下列问题：

（1）方案一中，y与x的函数关系式为                          ；
方案二中，当0≤x≤100时，y与x的函数关系式为                   ，
当x>100时，y与x的函数关系式为                       ；
（2）如果购买本场篮球赛门票超过100张，你将选择哪一种方案，使总费用最省?请说明理由；

如图，直线的解析表达式为，且与轴交于点D，直线经过点A，B，直线和交于点C．

（1）求直线的解析表达式；
（2）求△ADC的面积；
（3）直线上存在异于点C的另一点P，使△ADP与△ADC面积相等，求出点P的坐标．

某公司生产的某种商品每件成本为20元，经过市场调研发现，这种商品在未来40天内的日销售量m（件）与时间t（天）满足一次函数且关系如下表：

时间t（天）	1	3	6	10	36	…
日销售量m（件）	94	90	84	76	24	…

 
未来40天内，每天的销售价格y（元）与时间t（天）的函数关系式如下：

每天的销售价格y（元）	当1≤t≤20时，y1=t+25
当20＜t≤40时，y2=t+40

 
（1）求日销售量m（件）与时间t（天）的函数关系；
（2）请预测未来40天中哪一天的日销售利润最大，最大日销售利润是多少；
（3）在实际销售的前20天中，该公司决定每销售一件商品就捐赠a元（a＜4）给希望工程，公司通过销售记录发现，前20天中，每天扣除捐赠后的日销售利润随时间t（天）的增大而增大，求a的取值范围．

已知直线y=kx+b经过点A（5，0），B（1，4）．

（1）求直线AB的解析式；
（2）若直线y=2x-4与直线AB相交于点C，求点C的坐标；
（3）根据图象，写出关于x的不等式2x-4＞kx+b的解集．

“五一”期间，甲、乙两个家庭到300 km外的风景区“自驾游”， 乙家庭由于要携带一些旅游用品，比甲家庭迟出发0．5 h（从甲家庭出发时开始计时），甲家庭开始出发时以60 km/h的速度行驶．途中的折线、线段分别表示甲、乙两个家庭所走的路程y_甲（km）、y_乙（km）与时间x（h）之间的函数关系对应图象，请根据图象所提供的信息解决下列问题：

（1）由于汽车发生故障，甲家庭在途中停留了_______h；
（2）甲家庭到达风景区共花了多少时间？
（3）为了能互相照顾，甲、乙两个家庭在第一次相遇后约定两车之间的路程不超过15 km，请通过计算说明，按图所表示的走法是否符合约定．