如图，一次函数的图象与x轴，y轴分别相交于A，B两点，且与反比例函数y=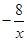
的图象在第二象限交于点C，其中点A（2，0），点B是AC的中点．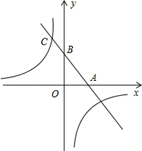
（1）求点C的坐标；
（2）求一次函数的解析式．
在平面直角坐标系中，如果点P的横坐标和纵坐标相等，则称点P为和谐点．例如点（1，1），（
，），（
，），…，都是和谐点．
（1）分别判断函数
和
的图象上是否存在和谐点，若存在，求出其和谐点的坐标；
（2）若二次函数
的图象上有且只有一个和谐点（
，），且当
时，函数
的最小值为－3，最大值为1，求
的取值范围；
（3）直线
经过和谐点P，与
轴交于点D，与反比例函数
的图象交于M，N两点（点M在点N的左侧），若点P的横坐标为1，且
，请直接写出
的取值范围．
如图，一次函数
的图象与反比例函数
（
为常数，且
）的图象都经过点A（m，2）．
（1）求点A的坐标及反比例函数的表达式；
（2）设一次函数的图象与x轴交于点B，若点P是x轴上一点，且满足△ABP的面积是2，直接写出点P的坐标．
设a，b是任意两个不等实数，我们规定：满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间，表示为[a，b]．对于一个函数，如果它的自变量x与函数值y满足：当m≤x≤n时，有m≤y≤n，我们就称此函数是闭区间[m．n]上的“闭函数”．如函数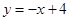
，当x=1时，y=3；当x=3时，y=1，即当
时，有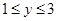
，所以说函数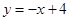是闭区间[1，3]上的“闭函数”．
（1）反比例函数y=
是闭区间[1，2015]上的“闭函数”吗？请判断并说明理由；
（2）若二次函数y=
是闭区间[1，2]上的“闭函数”，求k的值；
（3）若一次函数
（
）是闭区间[m，n]上的“闭函数”，求此函数的解析式（用含m，n的代数式表示）．
一农民带了若干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售．售出土豆千克数与他手中持有的钱数（含备用零钱）的关系如图所示，
结合图象回答下列问题：（1）农民自带的零钱是多少？（2）降价前他每千克土豆出售的价格是多少？（3）降价后他按每千克0.4元将剩余土豆售完，这时他手中的钱（含备用零钱）是26元，问他一共带了多少千克土豆？
如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y（元）与通话时间t（分钟）之间的函数关系的图象
（1）写出y与t之间的函数关系式．
（2）通话2分钟应付通话费多少元？通话7分钟呢？
如图，一次函数的图象经过A、B两点，与x轴交于点C，
（1）求直线AB的解析式
（2）求△AOC的面积.
（本小题满分8分）已知：在平面直角坐标系xOy中，给出如下定义：线段AB及点P，任取AB上一点Q，线段PQ长度的最小值称为点P到线段AB的距离，记作d（P→AB）．
（1）如图l，已知C点的坐标为（1，0），D点的坐标为（3，0），求点P（2，1）到线段CD的距离d（P→CD）为____；
（2）已知：线段EF：y=x（0≤x≤3），点G到线段时的距离d（P→EF）为
，且点G的横坐标为l，在图2中画出图，试求点G的纵坐标．
虽然近几年无锡市政府加大了太湖水治污力度，但由于大规模、高强度的经济活动和日益增加的污染负荷，使部分太湖水域水质恶化，富营养化不断加剧。为了保护水资源，我市制定一套节水的管理措施，其中对居民生活用水收费作如下规定：
| 月用水量（吨） |
单价（元/吨） |
| 不大于10吨部分 |
1．5 |
| 大于10吨不大于m吨部分（20≤m≤50） |
2 |
| 大于m吨部分 |
3 |
（1）若某用户六月份用水量为18吨，求其应缴纳的水费；
（2）记该用户六月份用水量为x吨，缴纳水费为y元，试列出y关于x的函数关系式；
（3）若该用户六月份用水量为40吨，缴纳水费y元的取值范围为70≤y≤90，试求m的取值范围．
为了调动同学们的学习积极性，某班班主任陈老师在班级管理中采用了奖励机制，每次期中期末考试后都会进行表彰奖励．期中考试后，陈老师花了300元购买甲、乙两种奖品用于奖励进步显著学生及成绩特别优秀学生．期末考试后，陈老师再次去购买奖品时，发现甲奖品每件上涨了6元，乙奖品每件上涨了12元，结果购买相同数量的甲、乙两种奖品却多花了120元．设陈老师每次购买甲奖品x件，乙奖品y件．
（1）请直接写出y与x之间的函数关系式： ．
（2）若x＝8，且这两种奖品不再调价．若陈老师再次去购买奖品，且所买甲奖品比前两次都少1件，则他最多买几件乙奖品，才能把奖品总费用控制在300元以内？
【备注：已知陈老师第一次购买奖品发现，甲奖品比乙奖品便宜，两种奖品单价（元）都在30以内且为偶数．】
如图1，已知直线y=2x+2与y轴、x轴分别交于A、B两点，以B为直角顶点在第二象限作等腰Rt△ABC
（1）求点C的坐标，并求出直线AC的关系式．
（2）如图2，直线CB交y轴于E，在直线CB上取一点D，连接AD，若AD=AC，求证：BE=DE．
（3）如图3，在（1）的条件下，直线AC交x轴于M，P（−
，k）是线段BC上一点，在线段BM上是否存在一点N，使直线PN平分△BCM的面积？若存在，请求出点N的坐标；若不存在，请说明理由．
一列快车由甲地开往乙地，一列慢车由乙地开往甲地，两车同时出发，匀速
运动．快车离乙地的路程y1（km）与行驶的时间x（h）之间的函数关系，如图中线段AB所示．慢车离甲地的路
程y2（km）与行驶的时间x（h）之间的函数关系，如图中线段AC所示．根据图像进行以下研究．
解读信息：（1）甲、乙两地之间的距离为 km；
（2）线段AB的解析式为 ； 两车在慢车出发 小时后相遇；
问题解决：
（3）设快、慢车之间的距离为y（km），求y与慢车行驶时间x（h）的函数关系式，并画出函数的图像．
为了迎接“五•一”小长假的购物高峰．某运动品牌专卖店准备购进甲、乙两
种运动鞋．其中甲、乙两种运动鞋的进价和售价如下表：
| 运动鞋价格 |
甲 |
乙 |
| 进价（元/双） |
m |
m﹣20 |
| 售价（元/双） |
240 |
160 |
已知：用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同．
（1）求m的值；
（2）要使购进的甲、乙两种运动鞋共200双的总利润（利润=售价﹣进价）不少于21700元，且不超过22300
元，问该专卖店有几种进货方案？
（3）在（2）的条件下，专卖店准备对甲种运动鞋进行优惠促销活动，决定对甲种运动鞋每双优惠a（50＜a＜70）元出售，乙种运动鞋价格不变．那么该专卖店要获得最大利润应如何进货？
粤公网安备 44130202000953号
