北京市燕山区中考一模数学试卷
据报道,中国内地首次采用“全无人驾驶”的燕房线地铁有望年底完工,列车通车后将极大改善房山和燕山居民的出行条件,预计年输送乘客可达7300万人次,将7300用科学记数法表示应为( )
A. |
B. |
C. |
D. |
下面是某小区居民家庭的月用水量情况统计表:
从中任意抽出一个家庭进行用水情况调查,则抽到的家庭月用水量为6吨的概率为( )
A. |
B. |
C. |
D. |
以下是期中考试后,班里两位同学的对话:
以上两位同学的对话反映出的统计量是( )
| A.众数和方差 | B.平均数和中位数 |
| C.众数和平均数 | D.众数和中位数 |
在多项式 中添加一个单项式,使其成为一个完全平方式,则添加的单项式可以是( )
中添加一个单项式,使其成为一个完全平方式,则添加的单项式可以是( )
| A.x | B.3x | C.6x | D.9x |
如图,⊙O的半径长6cm,点C在⊙O上,弦AB垂直平分OC于点D,则弦AB的长为( )
| A.9 cm | B. cm cm |
C. cm cm |
D. cm cm |
在△ABC中,按以下步骤作图:①分别以A,B为圆心,大于 AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠A=35°,则∠C=( )
AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠A=35°,则∠C=( )
A.40° B.50° C.60° D.70°
李阿姨每天早晨从家慢跑到小区公园,锻炼一阵后,再慢跑回家.表示李阿姨离开家的距离y (单位:米)与时间t (单位:分)的函数关系的图象大致如上图所示,则李阿姨跑步的路线可能是(用P点表示李阿姨家的位置)( )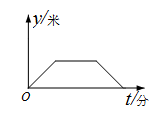
A.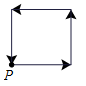 |
B.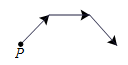 |
C.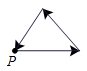 |
D.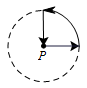 |
如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=45cm,当它的一端B着地时,另一端A离地面的高度AC为 cm.
为了节能减排,近期纯电动出租车正式上路运行.某地纯电动出租车的运价为3公里以内10元;超出3公里后每公里2元;单程超过15公里,超过部分每公里3元.小周要到离家10公里的博物馆参观,若他往返都乘坐纯电动出租车,共需付车费 元.
定义:对于任意一个不为1的有理数a,把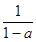 称为a的差倒数,如2的差倒数为
称为a的差倒数,如2的差倒数为 ,
,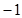 的差倒数为
的差倒数为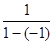 =
=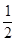 .记
.记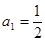 ,
,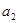 是
是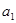 的差倒数,
的差倒数,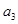 是
是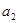 的差倒数,
的差倒数,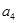 是
是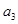 的差倒数,…,依此类推,则
的差倒数,…,依此类推,则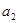 = ;
= ;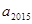 = .
= .
列方程或方程组解应用题:赵老师为了响应市政府“绿色出行”的号召,改骑自行车上下班,结果每天上班所用时间比自驾车多 小时.已知赵老师家距学校12千米,上下班高峰时段,自驾车的速度是自行车速度的2倍.求赵老师骑自行车的速度.
小时.已知赵老师家距学校12千米,上下班高峰时段,自驾车的速度是自行车速度的2倍.求赵老师骑自行车的速度.
如图,菱形ABCD中,对角线AC,BD交于O点,DE∥AC,CE∥BD.
(1)求证:四边形OCED为矩形;
(2)在BC上截取CF=CO,连接OF,若AC=8,BD=6,求四边形OFCD的面积.
根据国家邮政局相关信息,2014年我国快递业务量达140亿件,比2013年增长52%,跃居世界第一,而快递产生的包装垃圾也引起了邮政管理部门的重视.以下是根据相关数据绘制的统计图的一部分.
根据以上信息,解答下列问题:
(1)请补全条形统计图并标明相应数据;(结果保留整数)
(2)每件快递专用包装的平均价格约为1.2元,据此计算2014年全国直接丢弃的快递包装造成了约多少亿元的损失?
(3)北京市2014年的快递业务量约为6亿件,预计2015年的增长率与近五年全国快递业务量年增长率的平均值近似相等,据此估计2015年北京市快递业务量将达到_______亿件.(直接写出结果,精确到0.1)
如图,△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作⊙O的切线DE交AC于点E.
(1)求证:∠CDE=90°;
(2)若AB=13,sin∠C= ,求CE的长.
,求CE的长.
阅读下面材料:小军遇到这样一个问题:如图1,△ABC中,AB=6,AC=4,点D为BC的中点,求AD的取值范围.
(1)小军发现老师讲过的“倍长中线法”可以解决这个问题.他的做法是:如图2,延长AD到E,使DE=AD,连接BE,构造△BED≌△CAD,经过推理和计算使问题得到解决.
请回答:AD的取值范围是 .
(2)参考小军思考问题的方法,解决问题:如图3,△ABC中,E为AB中点,P是CA延长线上一点,连接PE并延长交BC于点D.求证:PA•CD=PC•BD.
抛物线 与
与 轴交于点C(0,3),其对称轴与
轴交于点C(0,3),其对称轴与 轴交于点A(2,0).
轴交于点A(2,0).
(1)求抛物线 的解析式;
的解析式;
(2)将抛物线 适当平移,使平移后的抛物线
适当平移,使平移后的抛物线 的顶点为D(0,
的顶点为D(0, ).已知点B(2,2),若抛物线
).已知点B(2,2),若抛物线 与△OAB的边界总有两个公共点,请结合函数图象,求
与△OAB的边界总有两个公共点,请结合函数图象,求 的取值范围.
的取值范围.
△ABC中,∠ABC=45°,AH⊥BC于点H,将△AHC绕点H逆时针旋转90°后,点C的对应点为点D,直线BD与直线AC交于点E,连接EH.

(1)如图1,当∠BAC为锐角时,
①求证:BE⊥AC;
②求∠BEH的度数;
(2)当∠BAC为钝角时,请依题意用实线补全图2,并用等式表示出线段EC,ED,EH之间的数量关系.
 的相反数是( )
的相反数是( )






 有意义,则x的取值范围是 .
有意义,则x的取值范围是 . = .
= .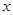 >0时,
>0时, 随
随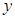 = .
= .
 .
.
 ,求代数式
,求代数式 的值.
的值. 的方程
的方程 .
. ,
, ,
,
 和
和 的图象上是否存在和谐点,若存在,求出其和谐点的坐标;
的图象上是否存在和谐点,若存在,求出其和谐点的坐标; 的图象上有且只有一个和谐点(
的图象上有且只有一个和谐点( ,
, 时,函数
时,函数 的最小值为-3,最大值为1,求
的最小值为-3,最大值为1,求 的取值范围;
的取值范围; 经过和谐点P,与
经过和谐点P,与 轴交于点D,与反比例函数
轴交于点D,与反比例函数 的图象交于M,N两点(点M在点N的左侧),若点P的横坐标为1,且
的图象交于M,N两点(点M在点N的左侧),若点P的横坐标为1,且 ,请直接写出
,请直接写出 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号