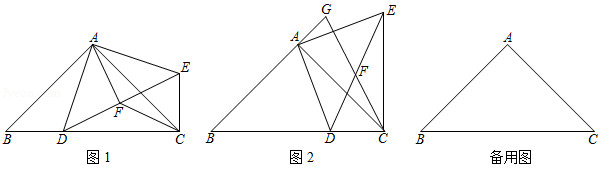
阅读下面材料：小军遇到这样一个问题：如图1，△ABC中，AB＝6，AC＝4，点D为BC的中点，求AD的取值范围．
（1）小军发现老师讲过的“倍长中线法”可以解决这个问题．他的做法是：如图2，延长AD到E，使DE＝AD，连接BE，构造△BED≌△CAD，经过推理和计算使问题得到解决．
请回答：AD的取值范围是 ．
（2）参考小军思考问题的方法，解决问题：如图3，△ABC中，E为AB中点，P是CA延长线上一点，连接PE并延长交BC于点D．求证：PA•CD＝PC•BD．
相关试题
+（－6）－
张慧同学给大家出了下面这样的问题，请你解答。
我的袋子里有3枚1角和1枚5角的硬币，如果我任意拿出两枚硬币，你知道前述之和大于5角的概率吗？
（要求：借助化树状图或列表的方法，列举所有等可能的结果，再进行计算。）
.
时，方程的两根之和为 ，两根之积为 
，求
的值；
是
的外接圆，点
在
上， 
，点
是垂足，
连接
．
推荐套卷
粤公网安备 44130202000953号