某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
| x(元) |
15 |
20 |
30 |
… |
| y(件) |
25 |
20 |
10 |
… |
若日销售量y是销售价x的一次函数.
(1)求出日销售量y(件)与销售价x(元)的函数关系式;
(2)要使每日销售利润最大,每件产品的销售价应定为多少元?此时,每日销售的利润是多少元?
(3)为了扩大销售量,经理决定每日销售的利润降到200元,每件产品的销售价应定为多少元?
如图,一次函数 与反比例函数
与反比例函数 的图象交于A(1,m)、B(4,n)两点.
的图象交于A(1,m)、B(4,n)两点.
(1)求A、B两点的坐标和反比例函数的解析式;
(2)根据图象,直接写出当y >y
>y 时x的取值范围;
时x的取值范围;
(3)求△AOB的面积.
某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
| x(元) |
15 |
20 |
30 |
… |
| y(件) |
25 |
20 |
10 |
… |
若日销售量y是销售价x的一次函数.
(1)求出日销售量y(件)与销售价x(元)的函数关系式;
(2)要使每日销售利润最大,每件产品的销售价应定为多少元?此时,每日销售的利润是多少元?
(3)为了扩大销售量,经理决定每日销售的利润降到200元,每件产品的销售价应定为多少元?
如图,一次函数y=-2x+3的图像交x轴于点A,交y轴于点B,点P在线段AB上(不与点A,B重合),过点P分别作OA和OB的垂线,垂足为C,D。点P在何处时,矩形OCPD的面积为1?
(本题8分)在平面直角坐标系中,直线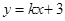 经过(2,7),求不等式
经过(2,7),求不等式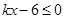 的解集.
的解集.
(本题8分)已知直线y=2x-b经过点(1,-1),求关于x的不等式2x-b≥0的解集.
两种移动电话计费方式表如下:
| |
全球通 |
神州行 |
| 月租费 |
15元/月 |
0 |
| 本地通话费 |
0.10元/分 |
0.20元/分 |
(1)一个月内某用户在本地通话时间为x分钟,请你用含有x的式子分别写出两种计费方式下该用户应该支付的费用;
(2)若某用户一个月内本地通话时间为5个小时,你认为采用哪种方式较为合算?
(3)小王想了解一下一个月内本地通话时间为多少时,两种计费方式的收费一样多.请你帮助他解决一下.
已知,如图,一次函数 与x轴、y轴分别交于点A和点B,A点坐标为(3,0),∠OAB=45°.
与x轴、y轴分别交于点A和点B,A点坐标为(3,0),∠OAB=45°.
(1)求一次函数的表达式;
(2)点P是x轴正半轴上一点,以P为直角顶点,BP为腰在第一象限内作等腰Rt△BPC,连接CA并延长交y轴于点Q.
①若点P的坐标为(4,0),求点C的坐标,并求出直线AC的函数表达式;
②当P点在x轴正半轴运动时,Q点的位置是否发现变化?若不变,请求出它的坐标;如果变化,请求出它的变化范围.
甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
(1)求出图中a的值;
(2)求出甲车行驶路程y(km)与时间x(h)的函数表达式,并写出相应的x的取值范围;
(3)当甲车行驶多长时间时,两车恰好相距40km.
某剧院举行专场音乐会,成人票每张20元,学生票每张5元,暑假期间,为了丰富广大师生的业余文化生活,剧院制定了两种优惠方案,方案一:购买一张成人票赠送一张学生票;方案二:按总价的90%付款,某校有4名老师与若干名(不少于4人)学生听音乐会.
(1)设学生人数为x(人),分别求出方案一、方案二的付款总金额 、
、 (元)与x的函数表达式;
(元)与x的函数表达式;
(2)学生人数在什么范围内,两种方案费用一样?人数在什么范围内,选方案一较划算?人数在什么范围内,选方案二较划算?
(本题10分)已知一次函数 的图像与x轴交于点A,与y轴交于点B(0,2),且与正比例函数
的图像与x轴交于点A,与y轴交于点B(0,2),且与正比例函数 的图像交于点C(
的图像交于点C(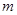 ,4)
,4)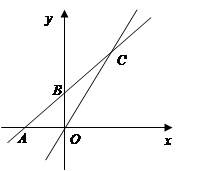
(1)求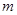 的值;
的值;
(2)求一次函数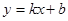 的表达式;
的表达式;
(3)求这两个函数图像与 轴所围成的△AOC的面积.
轴所围成的△AOC的面积.
如图,直线l1: 与x轴交于点B(1,0),直线l2:
与x轴交于点B(1,0),直线l2: 与y轴交于点C,这两条直线交于A(2,a).
与y轴交于点C,这两条直线交于A(2,a).
(1)直接写出a的值;
(2)求点C的坐标;
(3)求直线l1的表达式;
(4)求四边形ABOC的面积.
(本题10分)如图,一次函数 的图象与坐标轴分别交于A、B两点,与反比例函数
的图象与坐标轴分别交于A、B两点,与反比例函数 的图象在第二象限的交点为C,CD⊥x轴,垂足为D,若OB=2,OD=4,△AOB的面积为1.
的图象在第二象限的交点为C,CD⊥x轴,垂足为D,若OB=2,OD=4,△AOB的面积为1.
(1)求一次函数与反比例的表达式;
(2)直接写出当 时,
时, 的解集.
的解集.
元旦期间,甲、乙两个家庭到300 km外的风景区“自驾游”,乙家庭由于要携带一些旅游用品,比甲家庭迟出发0.5 h(从甲家庭出发时开始计时),甲家庭开始出发时以60 km/h的速度行驶.途中的折线、线段分别表示甲、乙两个家庭所走的路程y甲(km)、y乙(km)与时间x(h)之间的函数关系对应图象,请根据图象所提供的信息解决下列问题:
(1)由于汽车发生故障,甲家庭在途中停留了 h;
(2)甲家庭到达风景区共花了多少时间;
(3)为了能互相照顾,甲、乙两个家庭在第一次相遇后约定两车的距离不超过15 km,请通过计算说明,按图所表示的走法是否符合约定.