福建省福安市八年级上学期期末考试数学试卷
下列语句中,是命题的是( ).
| A.过直线l外一点作l的平行线 |
| B.美丽的天空 |
| C.你的作业做完了吗? |
| D.对顶角相等 |
以下列长度的三条线段为边,不能组成直角三角形的是( ).
| A.3,4,5 | B.6,8,10 | C.5,12,13 | D.1,1,2 |
下列说法正确的是( ).
| A.6.4的立方根是0.4 |
| B.-9的平方根是±3 |
C. 是无理数 是无理数 |
D. |
在平面直角坐标系中,点P的坐标为(4,5),则点P在( ).
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
下列数据不能确定物体的位置的是( ).
| A.南偏西40° | B.某电影院5排21号 |
| C.大桥南路38号 | D.北纬21°,东经115° |
已知点M(1,a)和点N(2,b)是一次函数 图象上的两点,则a与b的大小关系是( ).
图象上的两点,则a与b的大小关系是( ).
| A.a>b | B.a=b | C.a<b | D.以上都不对 |
实验学校九年级一班十名同学定点投篮测试,每人投篮六次,投中的次数统计如下:5,4,3,5,5,2,5,3,4,1,则这组数据的众数为( ).
| A.5 | B.4 | C.3 | D.2 |
已知,一次函数y=kx+b的图象如图所示,下列结论正确的是( ).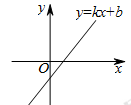
| A.k>0,b>0 | B.k>0,b<0 | C.k<0,b>0 | D.k<0,b<0 |
20位同学在植树节这天共种了52棵树苗,其中男生每人种3棵,女生每人种2棵.设男生有x人,女生有y人,根据题意,列方程组正确的是( ).
A.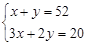 |
B.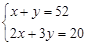 |
C.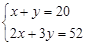 |
D. |
如图,正方形ABCD在平面直角坐标系中,其中三个顶点的坐标分别为A(-2,3),B(-2,-2),C(3,-2),则第四个顶点D的坐标为 .
甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如下表:
| 选手 |
甲 |
乙 |
丙 |
丁 |
| 平均数 |
9.2 |
9.2 |
9.2 |
9.2 |
| 方差 |
0.035 |
0.015 |
0.025 |
0.027 |
则这四人中射击成绩发挥最稳定的是 .
如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为 cm.(容器的厚度忽略不计)
如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,求∠3的度数.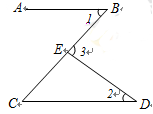
一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三方面为选手打分,各项成绩均按百分制,进入决赛的两名选手的单项成绩如下表所示:
| 选手 |
演讲内容 |
演讲能力 |
演讲效果 |
| 甲 |
85 |
95 |
95 |
| 乙 |
95 |
85 |
95 |
| |
演讲内容 |
演讲能力 |
演讲效果 |
| 甲 |
85 |
95 |
95 |
| 乙 |
95 |
85 |
95 |
(1)如果认为这三方面的成绩同等重要,从他们的成绩看,谁将胜出?
(2)如果按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例来计算甲、乙的平均成绩,那么谁将胜出?
身高1.6米的小明想利用“勾股定理”测得下图风筝CE的高度,于是他测得BD的长度为25米,并根据手中剩余线的长度计算出风筝线BC的长为65米.求风筝的高度CE.
小明爸爸骑摩托车带着小明在公路行驶,下图是小明在不同时间看到的里程碑情况.你能确定小明在12:00时看到的里程碑上的数吗?
如果设小明在12:00时看到的数的十位数字是x,个位数字是y,那么
(1)12:00时小明看到的数可表示为 ,
根据“两个数字之和是7”,可列出方程 ;
(2)13:00时小明看到的数可表示为 ,
根据“13:00时看到的两位数比12:00时看到的大45”,可列出方程 ;
(3)根据以上分析,得出方程组,并求出小明在12:00时看到的里程碑上的数.
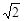 的绝对值是( ).
的绝对值是( ).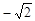
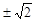
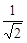

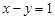 的一个解是 .
的一个解是 .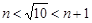 ,则n的值为 .
,则n的值为 .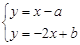 的解为
的解为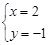 ,那么函数
,那么函数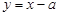 与
与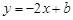 的交点坐标为 .
的交点坐标为 . ;
;
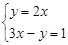 ; (2)
; (2)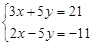 .
. 与x轴交于点B(1,0),直线l2:
与x轴交于点B(1,0),直线l2: 与y轴交于点C,这两条直线交于A(2,a).
与y轴交于点C,这两条直线交于A(2,a).
 粤公网安备 44130202000953号
粤公网安备 44130202000953号