某校为了解八年级300名学生期中考的数学成绩,随机抽查了该年级50名学生的期中考数学成绩进行分析,绘制了不完整的频数分布表和频数分布直方图.
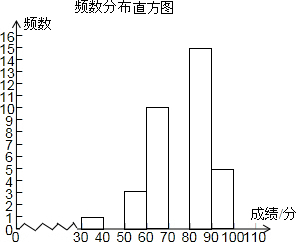
频数分布表
成绩分组
|
频 数
|
频 率
|
30≤x<40
|
1
|
0.02
|
40≤x<50
|
1
|
0.02
|
50≤x<60
|
3
|
|
60≤x<70
|
|
0.2
|
70≤x<80
|
15
|
0.3
|
80≤x<90
|
15
|
0.3
|
90≤x<100
|
5
|
0.1
|
合计
|
50
|
1
|
(1)以上分组的组距=;
(2)补全频数分布表和频数分布直方图;
(3)请你估计该校八年级期中考数学成绩优秀(不低于80分为优秀)的总人数.