如图，直线l1：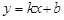
与x轴交于点B（1，0），直线l2：
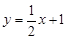与y轴交于点C，这两条直线交于A（2，a）．
（1）直接写出a的值；
（2）求点C的坐标；
（3）求直线l1的表达式；
（4）求四边形ABOC的面积．
相关试题
．
，其中
。
，求代数式
的值．
，
满足
，求
的值．
集，甲、乙两部连续剧的收视观众的人次的总和为
万人次，求相关知识点
推荐套卷
如图，直线l1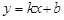：与x轴交于点B（1，0），直线l2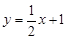：与y轴交于点C，这两条直线交于A（2，a）．
（1）直接写出a的值；
（2）求点C的坐标；
（3）求直线l1的表达式；
（4）求四边形ABOC的面积．
粤公网安备 44130202000953号