山东省济南市槐荫区九年级阶段性测试(一模)数学试卷
我国经济飞速发展,2014年的GDP为63.6万亿元,用科学记数法表示63.6万亿元为
| A.0.636×106亿元 | B.6.36×105亿元 |
| C.6.36×104亿元 | D.63.6×105亿元 |
如图,BD平分∠ABC,点E在BC上,EF∥AB.若∠CEF=100°,则∠ABD的度数是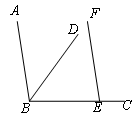
A.60° B.50° C.40° D.30°
5.一组数据-1、2、1、0、3的中位数和平均数分别是
| A.1,0 | B.2,1 | C.1,2 | D.1,1 |
若a<b,下列式子不成立的是
| A.a+1<b+1 |
| B.3a<3b |
| C.如果c<0,那么ac<bc |
| D.-0.5a>-0.5b |
已知 ABCD的周长为40,AB=BC-2,则对角线AC的取值范围为
ABCD的周长为40,AB=BC-2,则对角线AC的取值范围为
| A.2<AC<20 | B.2<AC<40 | C.10<AC<20 | D.5<AC<21 |
如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为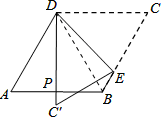
| A.30° | B.45° | C.60° | D.75° |
已知M、N两点关于y轴对称,且点M在双曲线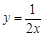 上,点N在直线
上,点N在直线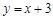 上,设点M的坐标为(a,b),则二次函数
上,设点M的坐标为(a,b),则二次函数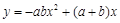
| A.有最大值-4.5 | B.有最大值4.5 |
| C.有最小值4.5 | D.有最小值-4. |
用图象法解某二元一次方程组时,如图所示在同一直角坐标系中作出相应的两个一次函数的图象,则所解的二元一次方程组是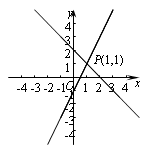
A.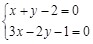 |
B.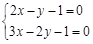 |
C.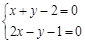 |
D.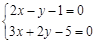 |
如图,将△ABC绕点P顺时针旋转90°得到△A′B′C′,则点P的坐标是
| A.(1,1) | B.(1,2) | C.(1,3) | D.(1,4) |
如图,在矩形ABCD中,AB=6,BC=8,点E是BC中点,点F是边CD上的任意一点,当△AEF的周长最小时,则DF的长为
| A.1 | B.2 | C.3 | D.4 |
如图,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数y=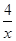 (x>0)的图象分别交于点B1、B2、B3,分别过点B1、B2、B3作x轴的平行线,分别与y轴交于点C1、C2、C3,连结OB1、OB2、OB3,那么图中阴影部分的面积之和为
(x>0)的图象分别交于点B1、B2、B3,分别过点B1、B2、B3作x轴的平行线,分别与y轴交于点C1、C2、C3,连结OB1、OB2、OB3,那么图中阴影部分的面积之和为 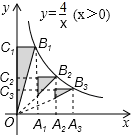
某初中学校共有学生720人,该校有关部门从全体学生中随机抽取了50人,对其到校方式进行调查,并将调查结果制成了如图所示的条形统计图,由此可以估计全校坐公交车到校的学生有 人.
下列条件之一能使□ABCD是菱形的有_____________________.(只填序号即可)
(1)AC⊥BD;(2)∠BAD=90°;(3)AB=CB;(4)AC=BD.
如图,扇形OAB和扇形OCD所在的圆是同心圆,其圆心为O,OA=2,∠COA=15°,∠AOB=60°,则阴影部分的面积为_____________.
如图,双曲线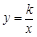 (x>0)经过点A(1,6)、点B(2,n),点P的坐标为(t,0),且-1≤t<3,则△PAB的最大面积为_______________.
(x>0)经过点A(1,6)、点B(2,n),点P的坐标为(t,0),且-1≤t<3,则△PAB的最大面积为_______________.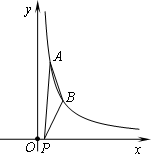
(1)已知:如图1,在Rt△ABC中,∠C=90°,BC=4,tanB= .求sinA的值.
.求sinA的值.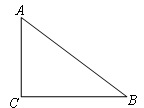
(2)已知:如图2,点E是正方形ABCD内一点,△CDE是等边三角形,连接EB、EA.求证:△ADE≌△BCE;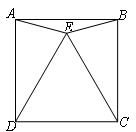
光明中学初三(2)班的同学积极响应学生会创办“书香班级”活动的倡议,将家中藏书带到学校,班里共收到文学类图书300本、科技类图书400本,文学类书籍平均每人的本数比科技类书籍少两本.问初三(2)班有多少名同学?
设方程 的两个根为x1、x2,令
的两个根为x1、x2,令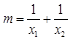 ,
,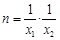 ,若点P的横坐标和纵坐标为x1、x2、m、n这四个数中任意两个数,则点P落在第二象限的概率是多少?
,若点P的横坐标和纵坐标为x1、x2、m、n这四个数中任意两个数,则点P落在第二象限的概率是多少?
因南方旱情严重,乙水库的蓄水量以每天相同的速度持续减少.为缓解旱情,北方甲水库立即以管道运输的方式给予支援.下图是两水库的蓄水量y(万米3)与时间x(天)之间的函数图象.在单位时间内,甲 水库的放水量与乙水库的进水量相同(水在排放、接收以及输送过程中的损耗不计).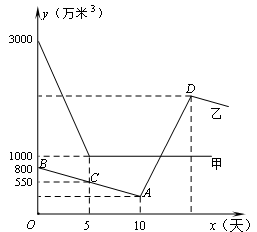
通过分析图象回答下列问题:
(1)甲水库每天的放水量是多少万立方米?
(2)在第几天时甲水库输出的水开始注入乙水库?此时乙水库的蓄水量为多少万立方米?
(3)求直线AD的解析式.
如图,线段AB=6,以AB为直径作半圆,点O为圆心,点P为半圆上任意一点(不与点A、点B重合),直线MN为过点P的切线,分别连接AP、BP,作AD⊥MN于点D,BC⊥MN于点C.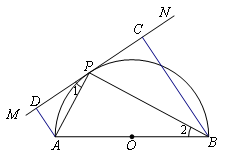
(1)求证:∠1=∠2.
(2)AD+BC的值是否为定值?如果是,求出这个定值;如果不是,请说明理由.
(3)求四边形ABCD面积的最大值.

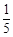

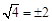
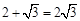
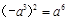
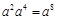

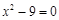
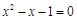
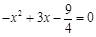
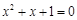
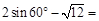 .
.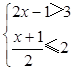 (2)化简:
(2)化简: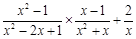
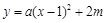 (m>0)经过点A(0,m),与x轴交于点B、点C,抛物线的对称轴交抛物线和x轴于点D、点E.
(m>0)经过点A(0,m),与x轴交于点B、点C,抛物线的对称轴交抛物线和x轴于点D、点E.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号