期中备考九年级数学模拟测试提升版【人教版】1
【原创】观察下列汽车图标,其中既是轴对称图形又是中心对称图形的有 ( )个.





| A.5个 | B.4个 | C.3个 | D.2个 |
中国航母辽宁舰是中国人民海军第一艘可以搭载固定翼飞机的航空母舰,满载排水量为67500吨,将67500用科学记数法表示为( )
| A.6.75×104吨 | B.67.5×103吨 |
| C.0.675×103吨 | D.6.75×10-4吨 |
函数y= 中,自变量x的取值范围是( ).
中,自变量x的取值范围是( ).
| A.x≠0 | B.x≥2 | C.x>2且x≠0 | D.x≥2且x≠0 |
下列运算正确的是( ).
| A.x2•x3=x6 | B.x6÷x5=x | C.(﹣x2)4=x6 | D.x2+x3=x5 |
【改编】在△ABC中,∠C=90°,∠B=∠22.5°,DE垂直平分AB交BC于E,BC=2+2 ,则 AC=( )
,则 AC=( )

| A.1 | B.2 | C.3 | D.4 |
【改编】如图,在△ABC中,两条中线BE、CD相交于点O,S△DOE=a,S△ABC=( ).

| A.4a | B.8a | C.9a | D.12a |
如图,在平面直角坐标系中,直线y= 与矩形ABCO的边OC、BC分别交于点E、F,已知OA=3,OC=4,则△CEF的面积是( )
与矩形ABCO的边OC、BC分别交于点E、F,已知OA=3,OC=4,则△CEF的面积是( )

A.6 B.3 C.12 D.
已知:在△ABC中,BC=10,BC边上的高h=5,点E在边AB上,过点E作EF∥BC,交AC边于点F.点D为BC上一点,连接DE、DF.设点E到BC的距离为x,则△DEF的面积S关于x的函数图象大致为( ).
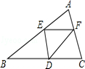

在矩形ABCD中,AB=1,AD= ,AF平分∠DAB,过C点作CE
,AF平分∠DAB,过C点作CE BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )

| A.1个 | B.2个 | C.3个 | D.4个 |
【改编】点E(a,-5)与点F(-2,b)关于y轴对称,则(2a+b)2015=__________.
【改编】箱子中装有6个只有颜色不同的球,其中1个红球,m个黄球,n个白球.从箱子中随机摸出一个球不是白球的概率是 ,不是黄球的概率是
,不是黄球的概率是 ,则mn=
,则mn=
如图,半径为6cm 的⊙O中,C,D为直径AB 的三等分点,点E,F分别在AB两侧的半圆上,∠BCE =∠BDF = 60°,连结AE,BF.则图中两个阴影部分的面积和
为 cm2.

如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数 的图象上.若点A的坐标为(-2,-2),则k的值为
的图象上.若点A的坐标为(-2,-2),则k的值为

服装店销售某款服装,一件服装的标价为300元,若按标价的八折销售,仍可获利60元,则这款服装每件的标价比进价多 元.
正方形 、
、 、
、 、… ,按如图所示的方式放置.点
、… ,按如图所示的方式放置.点 、
、 、
、 、…和点
、…和点 、
、 、
、 、…分别在直线
、…分别在直线 和
和 轴上,则第2015个正方形
轴上,则第2015个正方形 的边长为_____________.
的边长为_____________.
如图,已知△ABC的三个顶点的坐标分别 为A(-6,0)、B(-2,3)、C(-1,0).
(1)将△ABC绕坐标原点O逆时针旋转90°.画出对应的△A′B′C′图形;
(2)若四边形A′B′C′D′为平行四边形,请直接写出第四个顶点D′的坐标.
【改编】如图,己知:反比例函数 的图象与一次函数y=mx+b的图象交于点A(1,4),点B(-4,n).
的图象与一次函数y=mx+b的图象交于点A(1,4),点B(-4,n).
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积.
(3)在直线AB上是否存在点P,使得△AOP是以OP为腰的等腰三角形,若存在,直接写出点P的坐标,若不存在,说明理由.
我市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.市实验中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图:

(1)本次被调查的学生有 名;
(2)补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图2中所占圆心角的度数;
(3)该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?
已知关于 的一元二次方程
的一元二次方程
(1)求证:无论 取什么实数值,该方程总有两个不相等的实数根;
取什么实数值,该方程总有两个不相等的实数根;
(2)当Rt△ABC的斜边 ,且两条直角边的长 b和c恰好是这个方程的两个根,求
,且两条直角边的长 b和c恰好是这个方程的两个根,求 的值
的值
【原创】为创建国家级文明卫生城市,搞好“大美伊春,天然氧吧”的宣传活动,我市园林部门计划用不超过2950盆甲种花卉和2470盆乙种花卉,组建中、小型两类盆景50个.已知组建一个中型盆景需甲种花卉75盆,乙种花卉45盆;组建一个小型盆景需甲种花卉35盆,乙种花卉55盆.
(1)问符合题意的组建方案有几种?请你帮园林部门设计出来;
(2)若组建一个中型盆景的费用是920元,组建一个小型盆景的费用是630元,试说明在(1)中哪种方案费用最低?最低费用是多少元?
如图,平面直角坐标系xOy中,一次函数y=- x+b(b为常数,b>0)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴相交于点C,与y轴相交于点D、E,点D在点E上方.
x+b(b为常数,b>0)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴相交于点C,与y轴相交于点D、E,点D在点E上方.
(1)若直线AB与 有两个交点F、G.
有两个交点F、G.
①求∠CFE的度数;
②用含b的代数式表示FG2,并直接写出b的取值范围;
(2)设b≥5,在线段AB上是否存在点P,使∠CPE=45°?若存在,请求出P点坐标;若不存在,请说明理由.
 的值为5,则代数式
的值为5,则代数式 的值是 ( )
的值是 ( ) )2014×(
)2014×( -2)2015=
-2)2015=  =0,则此三角形最长边上的中线= ;最长边上的高= .
=0,则此三角形最长边上的中线= ;最长边上的高= . 的两个根,则a2-5a-b+ab= .
的两个根,则a2-5a-b+ab= . 的图象的一部分,请你根据图象写出方程
的图象的一部分,请你根据图象写出方程 的两根是 .
的两根是 .
 ,其中a=
,其中a= +1,b=
+1,b= 与x轴的两个交点分别为A(-3,0),B(1,0),过顶点C作CH⊥x轴于点H.
与x轴的两个交点分别为A(-3,0),B(1,0),过顶点C作CH⊥x轴于点H.


 轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由.
轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号