在平面直角坐标系中,抛物线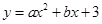 与x轴的两个交点分别为A(-3,0),B(1,0),过顶点C作CH⊥x轴于点H.
与x轴的两个交点分别为A(-3,0),B(1,0),过顶点C作CH⊥x轴于点H.

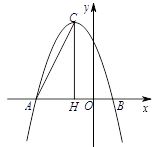

(1)a= ,b= ,顶点C的坐标为 .
(2)在 轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由.
轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由.
(3)若点P为x轴上方的抛物线上一动点(点P与顶点C不重合),PQ⊥AC于点Q,当△PCQ与△ACH相似时,求点P的坐标.
相关知识点
推荐套卷
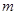 ∥
∥ ∥k,平行线l与
∥k,平行线l与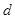 1、
1、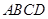 为“格线四边形”,
为“格线四边形”, 于点
于点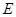 ,
,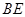 的反向延长线交直线k于点
的反向延长线交直线k于点 . 求正方形
. 求正方形 =60°,△
=60°,△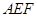 是等边三角形,
是等边三角形, 于点
于点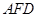 =90°,直线
=90°,直线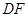 分别交直线l、k于点
分别交直线l、k于点 、
、 .求证:
.求证: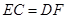 .
.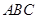 的顶点
的顶点 、
、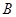 分别落在直线l、k上,
分别落在直线l、k上,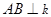 于点
于点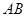 ="4" ,∠
="4" ,∠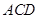 =90°,直线
=90°,直线 分别交直线l、k于点
分别交直线l、k于点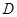 、
、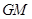 、
、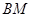 上的动点,且始终保持
上的动点,且始终保持 =
=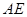 ,
, 于点
于点 .
. 在什么范围内,
在什么范围内, ∥
∥ ?直接写出结论。
?直接写出结论。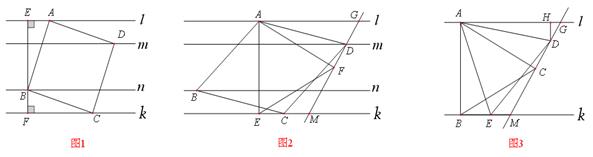
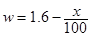 ,若想将模型作为教具卖出,且制作的长方体的个数不超过立方体的个数,则应该制作立方体和长方体各多少个,使获得的利润最大?最大利润是多少?
,若想将模型作为教具卖出,且制作的长方体的个数不超过立方体的个数,则应该制作立方体和长方体各多少个,使获得的利润最大?最大利润是多少?
 的图象过(0,-6)、(1,0)和(-2,-6)三点.
的图象过(0,-6)、(1,0)和(-2,-6)三点.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号